题目内容
14.已知圆C1:x2+y2+2x+3y+1=0,圆C2:x2+y2+4x+3y+2=0,则圆C1、圆C2的公切线有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 分别求出圆C1和圆C2的圆心与半径,从而判断出圆C1和圆C2相交,由此能求出圆C1、圆C2的公切线有多少条.
解答 解:∵圆C1:x2+y2+2x+3y+1=0的圆心C1(-1,-$\frac{3}{2}$),半径r1=$\frac{1}{2}\sqrt{4+9-4}$=3,
圆C2:x2+y2+4x+3y+2=0的圆心${C}_{2}(-2,-\frac{3}{2})$,半径${r}_{2}=\frac{1}{2}\sqrt{16+9-8}$=$\frac{\sqrt{17}}{2}$,
|C1C2|=$\sqrt{(-1+2)^{2}+(-\frac{3}{2}+\frac{3}{2})^{2}}$=1,
∵3-$\frac{\sqrt{17}}{2}$<|C1C2|<3+$\frac{\sqrt{17}}{2}$,
∴圆C1和圆C2相交,
∴圆C1、圆C2的公切线有2条.
故选:B.
点评 本题考查两圆的公切线条数的求法,是基础题,解题时要认真审题,注意两圆位置关系的合理运用.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
4.如图给出的是计算$1+\frac{1}{3}+\frac{1}{5}+…+\frac{1}{2015}$的值的程序框图,其中判断框内应填入的是( )
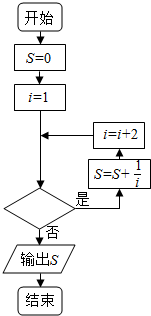

| A. | i≤2012 | B. | i≤2014 | C. | i≤2016 | D. | i≤2018 |
5.已知集合 M=Z(整数集)和${N}=\left\{{i,{i^2},\frac{1}{i},\frac{{{{({1+i})}^2}}}{i},\frac{{{{({1-i})}^2}}}{i}}\right\}$,其中i是虚数单位,则集合M∩N所含元素的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.如果(1-2x)7=a0+a1x+a2x2+…+a7x7,那么a0+a1+…+a7的值等于( )
| A. | -1 | B. | -2 | C. | 0 | D. | 2 |
6.设Sn是等差数列{an}的前n项和,若a4+a7=9,则S10=( )
| A. | 45 | B. | 40 | C. | 35 | D. | 30 |
3.命题“对任意的x∈R,都有x2-3=0”的否定为是( )
| A. | 存在x∉R,使x2-3=0 | B. | 存在x∈R,使x2-3≠0 | ||
| C. | 对任意的x∈R,都有x2-3≠0 | D. | 存在x∉R,使x2+3≠0 |
4.正方体ABCD-A1B1C1D1中,与侧棱AB异面且垂直的棱有( )
| A. | 8条 | B. | 6条 | C. | 4条 | D. | 3条 |