题目内容
9.如果(1-2x)7=a0+a1x+a2x2+…+a7x7,那么a0+a1+…+a7的值等于( )| A. | -1 | B. | -2 | C. | 0 | D. | 2 |
分析 利用赋值法求解即可.
解答 解:(1-2x)7=a0+a1x+a2x2+…+a7x7,
当x=1时,a0+a1+…+a7=(1-2)7=-1.
故选:A.
点评 本题考查二项式定理的应用,考查计算能力.

练习册系列答案
相关题目
19.若复数z满足(1-i)z=i,则复数z的模为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
17.函数f(x)=2x+3x-7的零点所在的区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
4.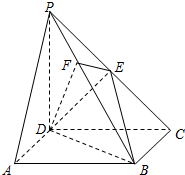 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(Ⅰ)求证:DE⊥平面PBC;
(Ⅱ)求二面角F-DE-B的正弦值.
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.(Ⅰ)求证:DE⊥平面PBC;
(Ⅱ)求二面角F-DE-B的正弦值.
14.已知圆C1:x2+y2+2x+3y+1=0,圆C2:x2+y2+4x+3y+2=0,则圆C1、圆C2的公切线有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
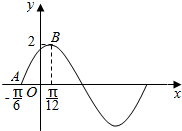 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示 (1)计算:${27^{\frac{2}{3}}}-{2^{{{log}_2}3}}×{log_2}\frac{1}{8}+2lg({\sqrt{3+\sqrt{5}}+\sqrt{3-\sqrt{5}}})$
(1)计算:${27^{\frac{2}{3}}}-{2^{{{log}_2}3}}×{log_2}\frac{1}{8}+2lg({\sqrt{3+\sqrt{5}}+\sqrt{3-\sqrt{5}}})$ 如图,正方体ABCD-A1B1C1D1的顶点A在平面α内,且直线AA1与平面α所成的角为45°,顶点A1在平面α上的射影为点O,当顶点C1与点O的距离最大时,直线C1B与平面α所成角的正弦值等于$\frac{2+\sqrt{2}}{4}$.
如图,正方体ABCD-A1B1C1D1的顶点A在平面α内,且直线AA1与平面α所成的角为45°,顶点A1在平面α上的射影为点O,当顶点C1与点O的距离最大时,直线C1B与平面α所成角的正弦值等于$\frac{2+\sqrt{2}}{4}$.