题目内容
5.已知集合 M=Z(整数集)和${N}=\left\{{i,{i^2},\frac{1}{i},\frac{{{{({1+i})}^2}}}{i},\frac{{{{({1-i})}^2}}}{i}}\right\}$,其中i是虚数单位,则集合M∩N所含元素的个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据复数的运算性质结合集合的运算判断即可.
解答 解:∵i2=-1,$\frac{1}{i}$=-i,$\frac{{(1+i)}^{2}}{i}$=2,$\frac{{(1-i)}^{2}}{i}$=-2,
∴M∩N={-2,-1,2},共3个元素,
故选:B.
点评 本题考察了复数的运算以及集合的运算,是一道基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
16.设集合A={x|x2-2x=0},B={x|x2+2x=0},则A∪B=( )
| A. | {0} | B. | {0,2} | C. | {0,-2} | D. | {2,0,-2} |
13.化简$\frac{{tan{{22}°}+tan{{23}°}}}{{1-tan{{22}°}tan{{23}°}}}$得( )
| A. | -1 | B. | $\frac{π}{4}$ | C. | 1 | D. | 2 |
10.某组织对男女青年是否喜爱古典音乐进行了一个调查,调查者随机调查了146名青年,下表给出了调查结果(单位:人)
(1)用分层抽样的方法在不喜爱古典音乐的青年中抽8人,其中男青年应抽几人?
(2)男女青年喜爱古典音乐的程度是否有差异?
| 喜爱古典音乐 青年 | 喜爱 | 不喜爱 |
| 男青年 | 46 | 30 |
| 女青年 | 20 | 50 |
(2)男女青年喜爱古典音乐的程度是否有差异?
17.函数f(x)=2x+3x-7的零点所在的区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
14.已知圆C1:x2+y2+2x+3y+1=0,圆C2:x2+y2+4x+3y+2=0,则圆C1、圆C2的公切线有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
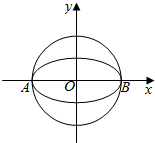 已知椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
已知椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.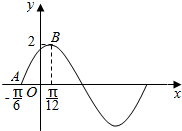 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示