题目内容
8.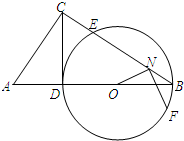 如图∠ACB=90°,CD⊥AB于点D,以BD为直径的⊙O与BC交于点E.
如图∠ACB=90°,CD⊥AB于点D,以BD为直径的⊙O与BC交于点E.(Ⅰ)求证:BC•CE=AD•DB;
(Ⅱ)若BE=4,点N在线段BE上移动,∠ONF=90°,NF与⊙O相交于点F,求NF的最大值.
分析 (Ⅰ)由∠ACB=90°,CD⊥AB于D,得到CD2=AD•DB,由此利用切割线定理能证明CE•CB=AD•DB.
(Ⅱ)由NF=$\sqrt{O{F}^{2}-O{N}^{2}}$,线段OF的长为定值,得到需求解线段ON长度的最小值,由此能求出结果.
解答 证明:(Ⅰ)在△ABC中,∠ACB=90°,CD⊥AB于D,
∴CD2=AD•DB,
∵CD是圆O的切线,
由切割线定理,得CD2=CE•CB,
∴CE•CB=AD•DB.
解:(Ⅱ)∵ON⊥NF,∴NF=$\sqrt{O{F}^{2}-O{N}^{2}}$,
∵线段OF的长为定值,即需求解线段ON长度的最小值,
弦中点到圆心的距离最短,此时N为BE的中点,点F与点B或E重合,
∴|NF|max=$\frac{1}{2}$|BE|=2.
点评 本题考查两组线段乘积相等的证明,考查线段长最小的求法,是中档题,解题时要认真审题,注意切割线定理的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.设a=log37,b=21.1,c=0.83.1,则( )
| A. | b<a<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
13.甲、乙等5人在9月3号参加了纪念抗日战争胜利70周年阅兵庆典后,在天安门广场排成一排拍照留念,甲和乙必须相邻的排法有( )种.
| A. | 24 | B. | 48 | C. | 72 | D. | 120 |
20.某几何体的三视图如图,其正视图中的曲线部分为半个圆弧,则该几何体的表面积为( )
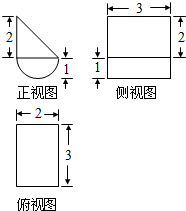

| A. | 16+6$\sqrt{2}$+4π | B. | 16+6$\sqrt{2}$+3π | C. | 10+6$\sqrt{2}$+4π | D. | 10+6$\sqrt{2}$+3π |
18.一个几何体的三视图如图所示,则该几何体的体积为( )
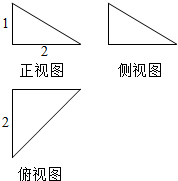

| A. | $\frac{4}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | 2 |