题目内容
16.在区间[-2,4]上随机地抽取一个实数x,若x满足x2≤m的概率为$\frac{5}{6}$,则实数m的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 9 |
分析 画出数轴,利用x满足x2≤m的概率为$\frac{5}{6}$,直接求出m的值即可.
解答  解:如图区间长度是6,区间[-2,4]上随机地取一个数x,若x满足x2≤m的概率为$\frac{5}{6}$,所以m=9.
解:如图区间长度是6,区间[-2,4]上随机地取一个数x,若x满足x2≤m的概率为$\frac{5}{6}$,所以m=9.
故选:D.
点评 本题考查几何概型的求解,画出数轴是解题的关键.

练习册系列答案
相关题目
5.设集合A={x||x-2|≤2,x∈R},B={x|-1≤x≤2},则∁R(A∩B) 等于( )
| A. | {x|-1<x<0} | B. | {x|2≤x<4} | C. | {x|x<0或x>2} | D. | {x|x≤0或x≥2} |
6.将函数$f(x)=sin({2x-\frac{π}{3}})$的图象向右平移$\frac{π}{3}$个单位得到函数g(x)的图象,则g(x)的一条对称轴方程可以为( )
| A. | $x=\frac{3π}{4}$ | B. | $x=\frac{7π}{6}$ | C. | $x=\frac{7π}{12}$ | D. | $x=\frac{π}{12}$ |
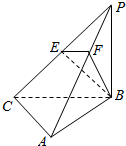 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.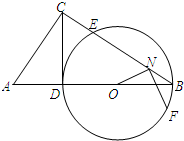 如图∠ACB=90°,CD⊥AB于点D,以BD为直径的⊙O与BC交于点E.
如图∠ACB=90°,CD⊥AB于点D,以BD为直径的⊙O与BC交于点E.