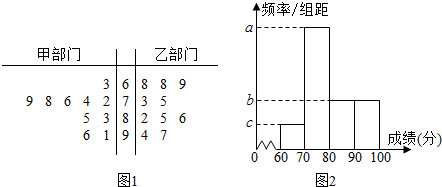
题目内容
18.一个几何体的三视图如图所示,则该几何体的体积为( )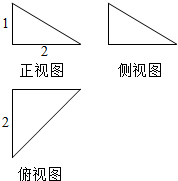
| A. | $\frac{4}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | 2 |
分析 几何体为三棱锥,棱锥的高为1,底面为直角边为2的等腰直角三角形.
解答 解:由三视图可知几何体为三棱锥,棱锥的高为1,底面为直角边为2的等腰直角三角形,
∴几何体的体积V=$\frac{1}{3}$×$\frac{1}{2}$×2×2×1=$\frac{2}{3}$.
故选:B.
点评 本题考查了三棱锥的三视图和体积计算,属于基础题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
9.“a=1”是函数f(x)=1-2sin2(ax+$\frac{π}{4}$)在区间($\frac{π}{12}$,$\frac{π}{6}$)上为减函数“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
6.将函数$f(x)=sin({2x-\frac{π}{3}})$的图象向右平移$\frac{π}{3}$个单位得到函数g(x)的图象,则g(x)的一条对称轴方程可以为( )
| A. | $x=\frac{3π}{4}$ | B. | $x=\frac{7π}{6}$ | C. | $x=\frac{7π}{12}$ | D. | $x=\frac{π}{12}$ |
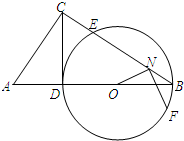 如图∠ACB=90°,CD⊥AB于点D,以BD为直径的⊙O与BC交于点E.
如图∠ACB=90°,CD⊥AB于点D,以BD为直径的⊙O与BC交于点E.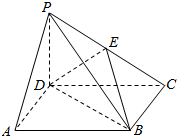 如图,四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.