题目内容
5.如图所示几何体的三视图,则该几何体的表面积为16+2$\sqrt{2}$.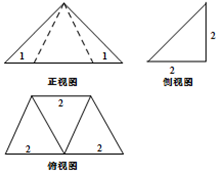
分析 由已知中的三视图,可得该几何体是一个以俯视图为底面的四棱锥,代入锥体表面积公式,可得答案.
解答 解:由已知中的三视图,可得该几何体是一个以俯视图为底面的四棱锥,
其直观图如下图所示: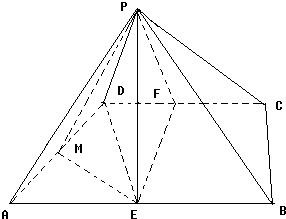
E和F分别是AB和CD中点,作EM⊥AD,连接PM,且PD=PC,
由三视图得,PE⊥底面ABCD,AB=4,CD=2,PE═EF=2
在直角三角形△PEF中,PF=$\sqrt{{EF}^{2}+{PE}^{2}}$=2$\sqrt{2}$,
在直角三角形△DEF中,DE=$\sqrt{{EF}^{2}+{DF}^{2}}$=$\sqrt{5}$,同理在直角梯形ADEF中,AD=$\sqrt{5}$,
根据△AED的面积相等得,$\frac{1}{2}$×AD×ME=$\frac{1}{2}$×AE×EF,解得ME=$\frac{4}{\sqrt{5}}$,
∵PE⊥底面ABCD,EM⊥AD,∴PM⊥AD,PE⊥ME,
在直角三角形△PME中,PM=$\sqrt{{EM}^{2}+{PE}^{2}}$=$\frac{6}{\sqrt{5}}$,
∴该四棱锥的表面积S=$\frac{1}{2}$×(4+2)×2+$\frac{1}{2}$×4×2+$\frac{1}{2}$×2×2$\sqrt{2}$+2×$\frac{1}{2}$×$\sqrt{5}$×$\frac{6}{\sqrt{5}}$=16+2$\sqrt{2}$.
故答案为:16+2$\sqrt{2}$.
点评 本题考查的知识点是棱锥的体积和表面积,简单几何体的直观图,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.复数z满足z(1-i)=-1-i,则|z+2|=( )
| A. | 3 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
16.下列说法正确的是( )
| A. | 若p:?x∈R,x2+3x+5>0,则¬p:?x0∈R,x02+3x0+5<0 | |
| B. | “若α=$\frac{π}{3}$,则cosα=$\frac{1}{2}$”的否命题是“若α=$\frac{π}{3}$,则cosα≠$\frac{1}{2}$” | |
| C. | 已知A,B是△ABC的两个内角,则“A>B”是“sinA>sinB”的充要条件 | |
| D. | 命题“p∨q为真”是命题“p∧q为真”的充分不必要条件 |
13.执行图的程序框图后,输出的结果为( )
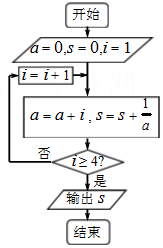

| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
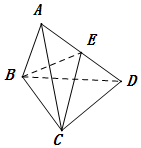 如图所示,△ABC和△BCD都是正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.
如图所示,△ABC和△BCD都是正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.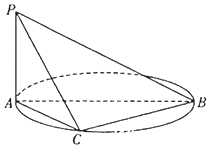 如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.
如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.