题目内容
设a是实数,f(x)=x2+ax+a,求证:|f(1)|与|f(2)|中至少有一个不小于
.
| 1 |
| 2 |
考点:反证法与放缩法,二次函数的性质
专题:证明题,反证法
分析:因“至少有一个不小于”的反面情况较简单,比较方便证明,故从反面进行证明.
解答:
证明:∵f(x)=x2+ax+a
∴f(1)=1+2a,f(2)=4+3a,
假设|f(1)|,|f(2)|都小于
,
则|1+2a|<
,|4+3a|<
∴-0.75<a<-0.25且-1.5<a<-
,不成立
∴假设不成立,即原命题成立.
∴f(1)=1+2a,f(2)=4+3a,
假设|f(1)|,|f(2)|都小于
| 1 |
| 2 |
则|1+2a|<
| 1 |
| 2 |
| 1 |
| 2 |
∴-0.75<a<-0.25且-1.5<a<-
| 7 |
| 6 |
∴假设不成立,即原命题成立.
点评:反证法是一种从反面的角度思考问题的证明方法,体现的原则是正难则反.反证法的基本思想:否定结论就会导致矛盾,证题模式可以简要的概括为“否定→推理→否定”.

练习册系列答案
相关题目
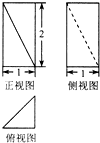
如图是某几何体的三视图,则该几何体的体积等于( )

A、
| ||
B、
| ||
| C、1 | ||
D、
|
函数y=log
(x2-3x+2)的单调递增区间为( )
| 1 |
| 2 |
| A、(-∞,1) | ||
B、(-∞,
| ||
C、[
| ||
| D、(2,+∞) |
如图是一个几何体的三视图,根据图中数据可得该几何体的体积是( )


A、
| ||
B、
| ||
| C、2 | ||
| D、4 |