题目内容
函数y=x2-4x-4的图象与x轴交于点A(x1,0),B(x2,0),与直线x+1=0交于点C,记过A,B,C三点的圆为⊙P.
(1)求⊙P的方程;
(2)直线l:x+y+m=0与⊙P交于点M,N,若PM⊥PN,求m的值.
(1)求⊙P的方程;
(2)直线l:x+y+m=0与⊙P交于点M,N,若PM⊥PN,求m的值.
考点:直线与圆锥曲线的关系,圆的标准方程,直线与圆的位置关系
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:(1)求出抛物线与x轴的交点AB坐标,C的坐标,然后求解圆⊙P的方程;
(2)直线l:x+y+m=0与⊙P交于点M,N,若PM⊥PN,判断三角形的形状,然后利用点到直线的距离公式得到方程求出m的值.
(2)直线l:x+y+m=0与⊙P交于点M,N,若PM⊥PN,判断三角形的形状,然后利用点到直线的距离公式得到方程求出m的值.
解答:
解:(1)y=x2-4x-4的图象与x轴交于点A(x1,0),B(x2,0),
则y=0时,x2-4x-4=0,解得A(2+2
,0),B(2-2
,0),
与直线x+1=0交于点C,可得C(-1,1).
过A,B,C三点的圆为⊙P,
圆的圆心横坐标为2,圆心设为(2,b),
可得(2+2
-2)2+(0-b)2=(-1-2)2+(1-b)2,
解得b=1,(-1-2)2+(1-1)2=9,圆的半径为:3
⊙P的方程:(x-2)2+(y-1)2=9.
(2)直线l:x+y+m=0与⊙P交于点M,N,若PM⊥PN,说明三角形PMN是等腰直角三角形,圆心到直线的距离为
r=
,由点到直线的距离可得:
=
,
解得m的值为:0或-6.
则y=0时,x2-4x-4=0,解得A(2+2
| 2 |
| 2 |
与直线x+1=0交于点C,可得C(-1,1).
过A,B,C三点的圆为⊙P,
圆的圆心横坐标为2,圆心设为(2,b),
可得(2+2
| 2 |
解得b=1,(-1-2)2+(1-1)2=9,圆的半径为:3
⊙P的方程:(x-2)2+(y-1)2=9.
(2)直线l:x+y+m=0与⊙P交于点M,N,若PM⊥PN,说明三角形PMN是等腰直角三角形,圆心到直线的距离为
| ||
| 2 |
3
| ||
| 2 |
| |2+1+m| | ||
|
3
| ||
| 2 |
解得m的值为:0或-6.
点评:本题考查直线与圆锥曲线的综合应用,直线与圆的位置关系,圆的方程的求法,考查计算能力.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
若a=
xdx,b=
dx,c=
2dx,则a,b,c的大小关系为( )
| ∫ | 4 2 |
| ∫ | 4 2 |
| 4 |
| x |
| ∫ | 4 2 |
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、c<b<a |
已知变量x,y满足约束条件
,若z=x-2y的最大值与最小值分别为a,b,且方程x2-kx+1=0在区间(b,a)有两解,则实数k的取值范围是( )
|
| A、(-6,-2) | ||
| B、(-3,2) | ||
C、(-
| ||
D、(-
|
已知全集U={x|0<x<9},A={x|1<x<a},若非空集合A⊆U,则实数a的取值范围是( )
| A、(-∞,9) |
| B、(-∞,9] |
| C、(1,9) |
| D、(1,9] |
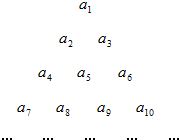 已知数列{an}中,a1=2,a5=10,an+2=2an+1-an(n∈N*),把数列{an}的各项排成如图所示的三角形状,记F(m,n)表示第m行、第n列的项,若F(m,n)+F(m+1,n+1)=90,则m+n=
已知数列{an}中,a1=2,a5=10,an+2=2an+1-an(n∈N*),把数列{an}的各项排成如图所示的三角形状,记F(m,n)表示第m行、第n列的项,若F(m,n)+F(m+1,n+1)=90,则m+n=