题目内容
试讨论并证明函数f(x)=
的单调性.
| 1-x2 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:由函数解析式f(x)=
可以知道该函数的定义域为[-1,1],由解析式的特点选择复合函数的求单调区间的方法求解即可.
| 1-x2 |
解答:
解:此函数可以看成是由函数y=f(t)=
和t=1-x2 复合而成,对于f(t)在t≥0始终单调递增,
对于t=1-x2,在x∈(-∞,0)上单调递增;在x∈[0,+∞)上单调递减,
有复合函数单调性的“同增异减”法则,可以知道:
当x∈[-1,0)时,函数f(x)是单调递增函数;
当0≤x≤1,即当x∈[0,1]时,函数f(x)是单调递减函数.
| t |
对于t=1-x2,在x∈(-∞,0)上单调递增;在x∈[0,+∞)上单调递减,
有复合函数单调性的“同增异减”法则,可以知道:
当x∈[-1,0)时,函数f(x)是单调递增函数;
当0≤x≤1,即当x∈[0,1]时,函数f(x)是单调递减函数.
点评:此题考查了复合函数的单调区间,用到了“同增异减”的法则去进行求函数的单调性.

练习册系列答案
相关题目
P是椭圆
+
=1(a>b>0)上的一个点,F为该椭圆的左焦点,O为坐标原点,且△POF为正三角形.则该椭圆离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、4-2
| ||||
B、2-
| ||||
C、
| ||||
D、
|

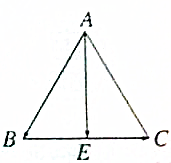 如图,已知△ABC是等边三角形.
如图,已知△ABC是等边三角形.