题目内容
已知数列{an}满足an+1=-
,a1=-
.
(1)求证{
}是等差数列;
(2)求数列{an}的通项公式;
(3)设Tn=an+an+1+…+a2n-1,若Tn≥p-n对任意的n∈N*恒成立,求p的最大值.
| 1 |
| an+2 |
| 1 |
| 2 |
(1)求证{
| 1 |
| an+1 |
(2)求数列{an}的通项公式;
(3)设Tn=an+an+1+…+a2n-1,若Tn≥p-n对任意的n∈N*恒成立,求p的最大值.
考点:数列递推式,函数恒成立问题
专题:等差数列与等比数列
分析:(1)由已知得an+1+1=-
+1=
=
,从而
=
=1+
,由此能证明{
}是以2为首项,以1为公差的等差数列.
(2)由(1)得
=2+(n-1)=n+1,由此能求出数列{an}的通项公式
(3)由已知得(1+an)+(1+an+1)+(1+an+2)+…+(1+a2n-1)≥p对任意n∈N*恒成立,由1+an=
,设H(n)=(1+an)+(1+an+1)+…+(1+a2n-1),推导出H(n+1)-H(n)>0,从而n∈N*时,H(n)≥H(1)=
,由此能求出P的最大值为
.
| 1 |
| an+2 |
| an+2-1 |
| an+2 |
| an+1 |
| an+2 |
| 1 |
| an+1+1 |
| an+2 |
| an+1 |
| 1 |
| an+1 |
| 1 |
| an+1 |
(2)由(1)得
| 1 |
| an+1 |
(3)由已知得(1+an)+(1+an+1)+(1+an+2)+…+(1+a2n-1)≥p对任意n∈N*恒成立,由1+an=
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
(1)证明:∵an+1=-
,a1=-
,
∴an+1+1=-
+1=
=
,
∵an+1=0与a1=-
矛盾,∴an+1≠0,
∴
=
=1+
,
又
=
=2,
∴{
}是以2为首项,以1为公差的等差数列.
(2)解:由(1)得
=2+(n-1)=n+1,
∴an=
-1=-
,n∈N*.
(3)解:∵Tn=an+an+1+…+a2n-1≥p-n,
∴n+an+an+1+…+a2n-1≥p,
∴(1+an)+(1+an+1)+(1+an+2)+…+(1+a2n-1)≥p对任意n∈N*恒成立,
而1+an=
,
设H(n)=(1+an)+(1+an+1)+…+(1+a2n-1),
∴H(n)=
+
+…+
,
H(n+1)=
+
+…+
+
+
,
∴H(n+1)-H(n)=
+
-
=
-
>0,
∴数列{H(n)}单调递增,
∴n∈N*时,H(n)≥H(1)=
,故P≤
,
∴P的最大值为
.
| 1 |
| an+2 |
| 1 |
| 2 |
∴an+1+1=-
| 1 |
| an+2 |
| an+2-1 |
| an+2 |
| an+1 |
| an+2 |
∵an+1=0与a1=-
| 1 |
| 2 |
∴
| 1 |
| an+1+1 |
| an+2 |
| an+1 |
| 1 |
| an+1 |
又
| 1 |
| a1+1 |
| 1 | ||
-
|
∴{
| 1 |
| an+1 |
(2)解:由(1)得
| 1 |
| an+1 |
∴an=
| 1 |
| n+1 |
| n |
| n+1 |
(3)解:∵Tn=an+an+1+…+a2n-1≥p-n,
∴n+an+an+1+…+a2n-1≥p,
∴(1+an)+(1+an+1)+(1+an+2)+…+(1+a2n-1)≥p对任意n∈N*恒成立,
而1+an=
| 1 |
| n+1 |
设H(n)=(1+an)+(1+an+1)+…+(1+a2n-1),
∴H(n)=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
H(n+1)=
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
∴H(n+1)-H(n)=
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
∴数列{H(n)}单调递增,
∴n∈N*时,H(n)≥H(1)=
| 1 |
| 2 |
| 1 |
| 2 |
∴P的最大值为
| 1 |
| 2 |
点评:本题考查等差数列的证明,考查数列的通项公式的求法,考查实数的最大值的求法,解题时要认真审题,注意构法和函数单调性的合理运用.

练习册系列答案
相关题目
已知定义在R上的函数f(x)=
,且f(x+2)=f(x),则方程f(x)=
在区间[-5,1]上的所有实数之和为( )
|
| 2x+5 |
| x+2 |
| A、-5 | B、-6 | C、-7 | D、-8 |
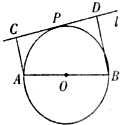 如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.