题目内容
16.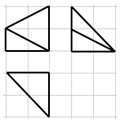 某几何体的三视图如图所示(网格线中,每个小正方形的边长为1),则该几何体的体积为( )
某几何体的三视图如图所示(网格线中,每个小正方形的边长为1),则该几何体的体积为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 根据几何体的三视图知该几何体是四棱锥,
结合图中数据求出该几何体的体积.
解答 解:根据几何体的三视图知,该几何体是如图所示的四棱锥,
则该几何体的体积为
V四棱锥P-ABCD=$\frac{1}{3}$×$\frac{1}{2}$×(1+2)×2×2=2.
故选:A.
点评 本题考查了几何体三视图的应用问题,是基础题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
19..已知数列{an}的通项公式为an=n•($\frac{3}{4}$)n,则数列{an}的最大项是( )
| A. | a1 | B. | a3 | C. | a5 | D. | 不能确定 |
4.函数f(x)=lg(|x|-1)的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
11.设函数$f(x)=-\frac{1}{3}{x}^{3}+x$在(t,10-t2)上有最大值,则实数t的取值范围为( )
| A. | $(-3,-\sqrt{6})$ | B. | $(-2,-\sqrt{3})$ | C. | [-2,1) | D. | (-2,1) |
1.一个几何体的三视图如图所示,其中俯视图为正方形,则该几何体最大的侧面的面积为( )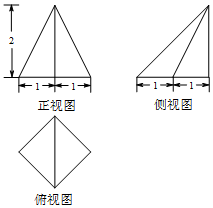

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
5.某几何体的三视图如图所示,则该几何体的体积为( )
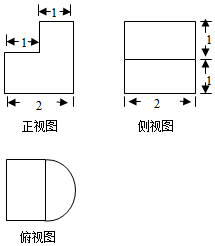

| A. | $\frac{1}{2}+\frac{π}{2}$ | B. | $1+\frac{π}{2}$ | C. | 1+π | D. | 2+π |
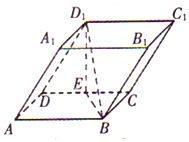 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.