题目内容
9.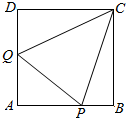 如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y.
如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y.(1)求x,y之间的函数关系式y=f(x);
(2)判断∠PCQ的大小是否为定值?并说明理由;
(3)设△PCQ的面积分别为S,求S的最小值.
分析 (1)由已知可得PQ=2-x-y,根据勾股定理有(2-x-y)2=x2+y2,即可求x,y之间的函数关系式y=f(x);
(2)求得∴∠DCQ+∠BCP=$\frac{π}{4}$,即可判断∠PCQ的大小;
(3)表示△PCQ的面积,利用基本不等式求S的最小值.
解答 解:(1)由已知可得PQ=2-x-y,根据勾股定理有(2-x-y)2=x2+y2,…(2分)
化简得:y=$\frac{2x-2}{x-2}$(0<x<1)…(3分)
(2)tan∠DCQ=1-y,tan∠BCP=1-x,…(5分)
tan(∠DCQ+∠BCP)=$\frac{2-x-y}{x+y-xy}$=1 …(7分)
∵∠DCQ+∠BCP∈(0,$\frac{π}{2}$),
∴∠DCQ+∠BCP=$\frac{π}{4}$,
∴∠PCQ=$\frac{π}{2}$-(∠DCQ+∠BCP)=$\frac{π}{4}$,(定值) …(8分)
(3)S=1-$\frac{1}{2}xy$-$\frac{1}{2}$(1-x)-$\frac{1}{2}$(1-y)=$\frac{1}{2}$(x+y-xy)=$\frac{1}{2}$•$\frac{{x}^{2}-2x+2}{2-x}$ …(10分)
令t=2-x,t∈(1,2),
∴S=$\frac{1}{2}$•(t+$\frac{2}{t}$)-1,
∴t=$\sqrt{2}$时,S的最小值为$\sqrt{2}$-1. …(12分)
点评 本题考查三角函数知识,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知圆的方程为x2+y2-2y-4=0,过点A(2,1)的直线被圆所截,则截得的最短弦的长度为( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $2\sqrt{2}$ |