题目内容
19.已知函数f(x)=$\frac{a}{2}$x2-(a+1)lnx+x+1.(1)当a<0时,讨论f(x)的单调性;
(2)若g(x)=$\frac{a+1}{2}$x2-a1nx-ax+1-f(x),设x1,x2(x1<x2)是函数g(x)的两个极值点,若a≥$\frac{3}{2}$,且g(x1)-g(x2)≥k恒成立,求实数k的最大值.
分析 (1)求出f(x)的导数,通过讨论a的范围,得到函数的单调性;(2)求函数的导数,根据函数极值之间的关系即可证明不等式.
解答 解:(1)f′(x)=ax-$\frac{a+1}{x}$+1=$\frac{(ax+a+1)(x-1)}{x}$,
①-$\frac{1}{2}$<a<0时,-$\frac{a+1}{a}$>1,
令f′(x)>0,解得:x>-$\frac{a+1}{a}$或0<x<1,
令f′(x)<0,解得:1<x<-$\frac{a+1}{a}$,
∴f(x)在(0,1),(-$\frac{a+1}{a}$,+∞)递增,在(1,-$\frac{a+1}{a}$)递减;
②-1≤a≤-$\frac{1}{2}$时,0<-$\frac{a+1}{a}$≤1,
令f′(x)>0,解得:x>1或0<x<-$\frac{a+1}{a}$,
令f′(x)<0,解得:-$\frac{a+1}{a}$<x<1
∴f(x)在(0,-$\frac{a+1}{a}$)递增,(-$\frac{a+1}{a}$,1)递减,在(1,+∞)递增;
③a<-1时,-$\frac{a+1}{a}$<0,
令f′(x)>0,解得:x>1,令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)递减,在(1,+∞)递增;
(2)∵g(x)=$\frac{a+1}{2}$x2-a1nx-ax+1-f(x)=)=lnx+$\frac{1}{2}$x2-(a+1)x,
∴g′(x)=$\frac{1}{x}$+x-(a+1)=$\frac{{x}^{2}-(a+1)x+1}{x}$,
由g′(x)=0得x2-(a+1)x+1=0
∴x1+x2=a+1,x1x2=1,
∴x2=$\frac{1}{{x}_{1}}$,
∵a≥$\frac{3}{2}$,∴$\left\{\begin{array}{l}{{x}_{1}+\frac{1}{{x}_{1}}≥\frac{5}{2}}\\{0{<x}_{1}<\frac{1}{{x}_{1}}}\end{array}\right.$,解得:0<x1≤$\frac{1}{2}$,
∴g(x1)-g(x2)=ln $\frac{{x}_{1}}{{x}_{2}}$+$\frac{1}{2}$(${{x}_{1}}^{2}$-${{x}_{2}}^{2}$)-(a+1)(x1-x2)=2lnx1-$\frac{1}{2}$(x12-$\frac{1}{{{x}_{1}}^{2}}$),
设F(x)=2lnx-$\frac{1}{2}$(x2-$\frac{1}{{x}^{2}}$)(0<x≤$\frac{1}{2}$),
则F′(x)=$\frac{2}{x}$-x-$\frac{1}{{x}^{3}}$=-$\frac{{{(x}^{2}-1)}^{2}}{{x}^{3}}$<0
∴F(x)在(0,$\frac{1}{2}$]上单调递减;
∴当x1=$\frac{1}{2}$时,F(x)min=F($\frac{1}{2}$)=$\frac{15}{8}$-2ln2,
∴k≤$\frac{15}{8}$-2ln2,
∴k的最大值为$\frac{15}{8}$-2ln2.
点评 本题主要考查导数的综合应用,求函数的导数,利用函数的极值,最值和导数之间是关系是解决本题的关键.综合性较强,运算量较大.

| A. | ($\frac{1}{2}$,+∞) | B. | (-2,-$\frac{1}{2}$) | C. | (-∞,-$\frac{1}{2}$) | D. | (-∞,-2) |
| A. | (-1,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
| A. | (4,-1,2) | B. | (-4,-1,2) | C. | (-4,1,2) | D. | (4,-1,-2) |
| A. | -$\frac{1}{3}$ | B. | -1 | C. | 1 | D. | $\frac{1}{2}$ |
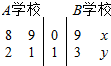 以下茎叶图记录了在高三一诊模拟考试中,A,B两个学校的各4个班的优生人数,其中有两个数据模糊不清,在图中用x,y表示,统计显示,A,B两个学校的优生人数的平均值相等,A校优生人数的方差比B校优生人数的方差小1.
以下茎叶图记录了在高三一诊模拟考试中,A,B两个学校的各4个班的优生人数,其中有两个数据模糊不清,在图中用x,y表示,统计显示,A,B两个学校的优生人数的平均值相等,A校优生人数的方差比B校优生人数的方差小1.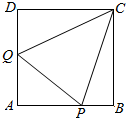 如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y.
如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y.