题目内容
4.已知函数f(x)=ln(1+x).(1)若函数g(x)=f(e4x)+ax,且g(x)是偶函数,求a的值;
(2)若h(x)=f(x)[f (x)+2m-1]在区间[e-1,e3-1]上有最小值-4,求m的值.
分析 (1)先求出g(x)=ln(1+e4x)+ax,由g(x)为偶函数,便可得到ln(1+e-4)-a=ln(1+e4)+a,这样便可求出a的值;
(2)可设f(x)=t,可得到t∈[1,3],设y=h(x),从而有$y={t}^{2}+(2m-1)t=[t-(\frac{1}{2}-m)]^{2}$$-{m}^{2}+m-\frac{1}{4}$,可讨论$\frac{1}{2}-m$和区间[1,3]的关系:分$\frac{1}{2}-m≤1,1<\frac{1}{2}-m<3$和$\frac{1}{2}-m≥3$三种情况,在每种情况里,根据y的最小值为-4便可建立关于m的方程,解方程即得m的值.
解答 解:(1)g(x)=f(e4x)+ax=ln(1+e4x)+ax,g(x)为偶函数;
∴g(-1)=g(1);
即ln(1+e-4)-a=ln(1+e4)+a;
∴ln(1+e4)-lne4-a=ln(1+e4)+a;
∴-4-a=a;
∴a=-2;
(2)令f(x)=t,x∈[e-1,e3-1],∴t∈[1,3];
设y=h(x),则y=${t}^{2}+(2m-1)t=[t-(\frac{1}{2}-m)]^{2}-{m}^{2}+m-\frac{1}{4}$;
①若$\frac{1}{2}-m≤1$,即$m≥-\frac{1}{2}$时,当t=1时,ymin=2m=-4;
∴m=-2与$m≥-\frac{1}{2}$不符;
②若$1<\frac{1}{2}-m<3$,即$-\frac{5}{2}<m<-\frac{1}{2}$时,当$t=\frac{1}{2}-m$时,${y}_{min}=-{m}^{2}+m-\frac{1}{4}=-4$;
解得m=$-\frac{3}{2}$,或$\frac{5}{2}$(舍去);
③若$\frac{1}{2}-m≥3$,即$m≤-\frac{5}{2}$时,当t=3时,
ymin=6m+6=-4;
∴$m=-\frac{5}{3}$,与$m≤-\frac{5}{2}$不符;
综上得,m的值为$-\frac{3}{2}$.
点评 考查已知f(x)求f[g(x)]的方法,偶函数的定义,换元法的应用,配方求二次函数最值的方法,根据二次函数的单调性求二次函数在闭区间上的最值.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案| A. | (-1,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
| A. | -$\frac{7}{10}$ | B. | $\frac{7}{10}$ | C. | -7 | D. | 7 |
| A. | y=|x| | B. | y=$\frac{1}{x}$ | C. | y=x3 | D. | y=2x |
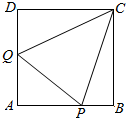 如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y.
如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y.