题目内容
20．已知函数f（x）=-x3+6x2-9x+8，则过点（0，0）可作曲线y=f（x）的切线的条数为（ ）| A． | 3 | B． | 0 | C． | 1 | D． | 2 |
分析 设出切点，求出切点处的导数，写出切线方程把A的坐标代入后得到关于切点横坐标的方程，再解方程即可判断切点横坐标的个数，从而答案可求．
解答 解：设切点为P（x0，-x03+6x02-9x0+8），
f（x）=-x3+6x2-9x+8的导数为f′（x）=-3x2+12x-9，
则f′（x0）=-3x02+12x0-9，
则切线方程y+x03-6x02+9x0-8=（-3x02+12x0-9）（x-x0），
代入O（0，0）得，x03-3x02+4=0，
即有（x0+1）（x0-2）2=0，解得x0=-1或2，
则切线有两条．
故选D．
点评 本题考查了利用导数研究曲线上点的切线问题，考查了利用切线方程，解方程的运算能力，是中档题．
练习册系列答案
相关题目
8．直线l1：x+（a+5）y-6=0与直线l2：（a-3）x+y+7=0互相垂直，则a等于（ ）
| A． | -$\frac{1}{3}$ | B． | -1 | C． | 1 | D． | $\frac{1}{2}$ |
5．曲线y=ex和曲线y=lnx分别与直线x=x0交于点A，B，且曲线y=ex在点A处的切线与曲线y=lnx在点B处的切线平行，则x0在下列哪个区间内（ ）
| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，4） |
12．已知向量$\overrightarrow{a}$=（λ+1，0，2），$\overrightarrow{b}$=（6，2μ-1，$\frac{2}{λ}$），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则λ+μ=（ ）
| A． | -$\frac{7}{10}$ | B． | $\frac{7}{10}$ | C． | -7 | D． | 7 |
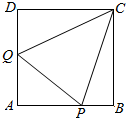如图，正方形ABCD的边长为1，P，Q分别为AB，DA上动点，且△APQ的周长为2，设 AP=x，AQ=y．