题目内容
1.若不等式$\frac{{x}^{2}-8x+20}{m{x}^{2}+2(m+1)x+9m+4}$>0对任意实数x恒成立,求m的取值范围.分析 由x2-8x+20=(x-4)2+4>0,可得mx2+2(m+1)x+4+9m>0,对任意实数x恒成立,对m讨论,当m=0,m>0,判别式小于0,m<0,解不等式即可得到所求范围.
解答 解:由x2-8x+20=(x-4)2+4>0,
可得mx2+2(m+1)x+4+9m>0,对任意实数x恒成立,
当m=0时,2x+4>0,解得x>-2,不恒成立;
当m>0,判别式4(m+1)2-4m(4+9m)<0,
解得m>$\frac{1}{4}$或m<-$\frac{1}{2}$,即有m>$\frac{1}{4}$成立;
当m<0时,不恒成立.
综上可得m的范围是($\frac{1}{4}$,+∞).
点评 本题考查不等式恒成立问题的解法,注意运用转化思想和二次不等式的解法,考查二次函数的图象和性质,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
12.已知向量$\overrightarrow{a}$=(λ+1,0,2),$\overrightarrow{b}$=(6,2μ-1,$\frac{2}{λ}$),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则λ+μ=( )
| A. | -$\frac{7}{10}$ | B. | $\frac{7}{10}$ | C. | -7 | D. | 7 |
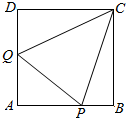 如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y.
如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y.