题目内容
17.已知关于x,y的方程C:x2+y2-2x-4y+m=0(Ⅰ)当方程C表示圆时,求m的取值范围;
(Ⅱ)若圆C与直线l1:x+2y-4=0相交于M,N两点,且|MN|=$\frac{6\sqrt{5}}{5}$,求m的值;
(Ⅲ)在(Ⅱ)条件下,若圆C上存在四点到直线l2:x-2y+b=0的距离均为$\frac{\sqrt{5}}{5}$,试求b的取值范围.
分析 (Ⅰ)由方程C:x2+y2-2x-4y+m=0变为(x-1)2+(y-2)2=5-m.当5-m>0表示圆,解出即可.
(2)利用点到直线的距离可得:圆心(1,2)到直线l的距离d,利用($\frac{3\sqrt{5}}{5}$)2+($\frac{1}{\sqrt{5}}$)2=5-m,即可解得m.
(3)如图所示,圆心(1,2)到直线l的距离d=$\frac{|c-3|}{\sqrt{5}}$,假设存在直线l:x-2y+b=0,使得圆上有四点到直线l的距离为$\frac{\sqrt{5}}{5}$,必须$\frac{|b-3|}{\sqrt{5}}$<|$\sqrt{2}$-$\frac{\sqrt{5}}{5}$|,解出即可.
解答 解:(Ⅰ)由方程C:x2+y2-2x-4y+m=0变为(x-1)2+(y-2)2=5-m
当5-m>0即m<5时,方程C表示圆;
(2)圆心(1,2)到直线l的距离d=$\frac{|1+4+4|}{\sqrt{5}}$=$\frac{1}{\sqrt{5}}$,
∵弦长|MN|=$\frac{6\sqrt{5}}{5}$,
∴($\frac{3\sqrt{5}}{5}$)2+($\frac{1}{\sqrt{5}}$)2=5-m,解得m=3.
故m=3.
(3)圆心(1,2)到直线l的距离d=$\frac{|c-3|}{\sqrt{5}}$,
假设存在直线l:x-2y+b=0,使得圆上有四点到直线l的距离为$\frac{\sqrt{5}}{5}$,
必须$\frac{|b-3|}{\sqrt{5}}$<|$\sqrt{2}$-$\frac{\sqrt{5}}{5}$|,解得4-$\sqrt{10}$<b<2+$\sqrt{10}$.
点评 本题考查了直线与圆的位置关系、弦长公式、勾股定理等基础知识与基本技能方法,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | -$\frac{1}{3}$ | B. | -1 | C. | 1 | D. | $\frac{1}{2}$ |
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
| A. | -$\frac{7}{10}$ | B. | $\frac{7}{10}$ | C. | -7 | D. | 7 |
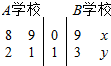 以下茎叶图记录了在高三一诊模拟考试中,A,B两个学校的各4个班的优生人数,其中有两个数据模糊不清,在图中用x,y表示,统计显示,A,B两个学校的优生人数的平均值相等,A校优生人数的方差比B校优生人数的方差小1.
以下茎叶图记录了在高三一诊模拟考试中,A,B两个学校的各4个班的优生人数,其中有两个数据模糊不清,在图中用x,y表示,统计显示,A,B两个学校的优生人数的平均值相等,A校优生人数的方差比B校优生人数的方差小1.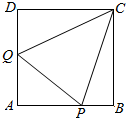 如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y.
如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y.