题目内容
14．已知圆的方程为x2+y2-2y-4=0，过点A（2，1）的直线被圆所截，则截得的最短弦的长度为（ ）| A． | $\frac{3}{2}$ | B． | 2 | C． | $\frac{{3\sqrt{2}}}{2}$ | D． | $2\sqrt{2}$ |
分析 根据题意可知，过A（2，1）的最长弦为直径，最短弦为过A（2，1）且垂直于该直径的弦，根据勾股定理求出最短弦的长度即可．
解答 解：圆的标准方程为x2+（y-1）2=5，
设过A（2，1）的最长的弦为直径，最短弦为过A（2，1））且垂直于直径的弦，弦心距为2，
根据勾股定理得最短的弦2$\sqrt{5-4}$=2，
故选：B．
点评 考查学生灵活运用垂径定理解决数学问题的能力．
练习册系列答案
相关题目
4．若空间向量$\overrightarrow{a}$=（1，-2，1），$\overrightarrow{b}$=（1，0，2），则下列向量可作为向量$\overrightarrow{a}$，$\overrightarrow{b}$所在平面的一个法向量的是（ ）
| A． | （4，-1，2） | B． | （-4，-1，2） | C． | （-4，1，2） | D． | （4，-1，-2） |
5．曲线y=ex和曲线y=lnx分别与直线x=x0交于点A，B，且曲线y=ex在点A处的切线与曲线y=lnx在点B处的切线平行，则x0在下列哪个区间内（ ）
| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，4） |
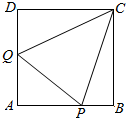如图，正方形ABCD的边长为1，P，Q分别为AB，DA上动点，且△APQ的周长为2，设 AP=x，AQ=y．
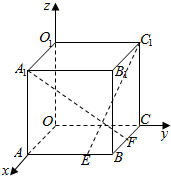如图，在棱长为a的正方体OABC-O1A1B1C1中，E，F分别是棱AB、BC上的动点，且AE=BF=x，其中0≤x≤a，以O为原点建立空间直角坐标系O-xyz．
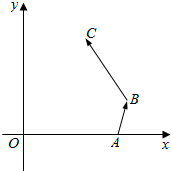如图，在平面直角坐标系中，|$\overrightarrow{OA}$|=2|$\overrightarrow{AB}$|=2，∠OAB=$\frac{2π}{3}$，$\overrightarrow{BC}$=（-1，$\sqrt{3}$）．