题目内容
曲线
-
=1与直线y=2x+m有两个交点,求m的取值范围.
| |x| |
| 2 |
| |y| |
| 2 |
考点:直线与圆锥曲线的关系
专题:计算题,数形结合,直线与圆
分析:作出直线和曲线对应的图象,根据图象关系即可确定m的取值范围.
解答:
 解:作出曲线对应的图象如图:由图象可知直线y=2x+m
解:作出曲线对应的图象如图:由图象可知直线y=2x+m
经过点A(-2,0)时,直线和曲线有一个交点,
此时-4+m=0,即m=4,此时要使两曲线有两个交点,则m>4,
直线y=2x+m经过点B(2,0)时,直线和曲线有一个交点,
当直线经过点B时,4+m=0,即m=-4,
此时要使两曲线有两个交点,则m<-4,
综上m的取值范围是m>4或m<-4.
 解:作出曲线对应的图象如图:由图象可知直线y=2x+m
解:作出曲线对应的图象如图:由图象可知直线y=2x+m经过点A(-2,0)时,直线和曲线有一个交点,
此时-4+m=0,即m=4,此时要使两曲线有两个交点,则m>4,
直线y=2x+m经过点B(2,0)时,直线和曲线有一个交点,
当直线经过点B时,4+m=0,即m=-4,
此时要使两曲线有两个交点,则m<-4,
综上m的取值范围是m>4或m<-4.
点评:本题主要考查曲线的交点问题的应用,利用数形结合,作出两个曲线的图象是解决本题的关键.

练习册系列答案
相关题目
若0<x<
,则x(1-2x)有( )
| 1 |
| 2 |
A、最小值
| ||
B、最小值
| ||
C、最大值
| ||
D、最大值
|
已知等差数列{an}的前n项和为Sn,S9=-18,S13=-52,{bn}为等比数列,且b5=a5,b7=a7,则b15的值为( )
| A、64 | B、128 |
| C、-64 | D、-128 |
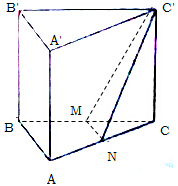 已知三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,侧楼AA1⊥底面ABC,AB=BC=CC1=4,N为AC的中点,M为BC的中点.
已知三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,侧楼AA1⊥底面ABC,AB=BC=CC1=4,N为AC的中点,M为BC的中点. 如图,在三棱锥S-ABC中,已知点E、F、G分别为棱SA、SC、BC的中点,过点E、F、G三点的平面与线段AB的交点为H.
如图,在三棱锥S-ABC中,已知点E、F、G分别为棱SA、SC、BC的中点,过点E、F、G三点的平面与线段AB的交点为H.