题目内容
已知函数f(x)=log
的图象关于原点对称,其中a为常数.
(1)求a的值;
(2)若当x∈(1,+∞)时,f(x)+log
(x-1)<m恒成立,求实数m的取值范围.
| 1 |
| 2 |
| 1-ax |
| x-1 |
(1)求a的值;
(2)若当x∈(1,+∞)时,f(x)+log
| 1 |
| 2 |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:(1)根据奇函数性质和对数的运算性质即可解得
(2)根据对数函数的单调性即可求出
(2)根据对数函数的单调性即可求出
解答:
解:(1)由题意可得,f(x)为奇函数,故有 f(-x)=-f(x),即log
=-log
,
∴
=1,
∴解得a=±1.
经检验,当a=1时不合条件,故a=-1.
(2)∵a=-1,
∴f(x)=log
,
∵当x∈(1,+∞)时,f(x)+log
(x-1)<m恒成立,
∴log
+log
(x-1)<m恒成立,
∴m>log
(x+1)在x∈(1,+∞)时,恒成立
∴m>log
(1+1)=-1
∴实数m的取值范围为(-1,+∞)
| 1 |
| 2 |
| 1-ax |
| x-1 |
| 1 |
| 2 |
| 1+ax |
| -x-1 |
∴
| 1-a2x2 |
| 1-x2 |
∴解得a=±1.
经检验,当a=1时不合条件,故a=-1.
(2)∵a=-1,
∴f(x)=log
| 1 |
| 2 |
| 1+x |
| x-1 |
∵当x∈(1,+∞)时,f(x)+log
| 1 |
| 2 |
∴log
| 1 |
| 2 |
| 1+x |
| x-1 |
| 1 |
| 2 |
∴m>log
| 1 |
| 2 |
∴m>log
| 1 |
| 2 |
∴实数m的取值范围为(-1,+∞)
点评:本题主要考查函数的奇偶性和单调性,函数恒成立的问题,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
某几何体的三视图如图所示,那么该几何体的表面积为( )
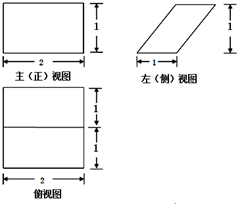

| A、2 | ||
| B、14 | ||
C、6+4
| ||
D、4+6
|
已知f(x)=2sin(2x+
)+1
(1)在直角坐标系中用“五点画图法”画出f(x)一个周期的图象(要求列表、描点)
(2)直接写出函数f(x)的单调递增区间以及f(x)取最大值时的所有x值的集合.
| π |
| 3 |
(1)在直角坐标系中用“五点画图法”画出f(x)一个周期的图象(要求列表、描点)
(2)直接写出函数f(x)的单调递增区间以及f(x)取最大值时的所有x值的集合.
已知命题p:当0<x<2时x2<4,命题q:当b<a<0时b2<a2,则( )
| A、p∧(¬q)为真 |
| B、p∧q为真 |
| C、(¬p)∨q为真 |
| D、(¬p)∧q为真 |
在棱长都相等的四面体ABCD中,M,N分别为BC,CD的中点,则MN与AC所成角为( )
| A、30° | B、45° |
| C、60° | D、90° |
某物体以40m/s初速度开始做减速运动,t秒时刻的速度v=40-10t2,则物体停止时经过的路程为( )
A、
| ||
B、
| ||
C、
| ||
D、
|