题目内容
14.定义在R上的函数f(x)的导函数是f′(x),若f(x)=f(2-x),且当x∈(-∞,1)时,(x-1)f′(x)<0,设a=f($\frac{1}{e}$)(e为自然对数的底数)、b=f($\sqrt{2}$)、c=f(log28),则( )| A. | c<a<b | B. | a>b>c | C. | a<b<c | D. | a<c<b |
分析 先由x∈(-∞,1)时,(x-1)f′(x)<0,得函数f(x)在(-∞,1)上为增函数;又f(x)=f(2-x)得f(x)图象关于x=1对称,则 f(x)在(1,+∞)上为减函数,然后将f($\frac{1}{e}$),f($\sqrt{2}$),f(log28)化到同一单调区间内比较即可.
解答 解:∵x∈(-∞,1)时,
∴(x-1)f′(x)<0,
∴f′(x)>0,
∴f(x)在(-∞,1)上为增函数,
又∵f(x)=f(2-x),
∴f(x)图象关于x=1对称,
∴f(x)在(1,+∞)上为减函数,
又∵a=f($\frac{1}{e}$)=f(2-$\frac{1}{e}$),b=f($\sqrt{2}$),c=f(log28)=f(3),
∴3>2-$\frac{1}{e}$>$\sqrt{2}$,
∴c<a<b.
故选:A.
点评 解题的关键为由f(x)=f(2-x)得函数图象关于x=1对称,以及利用导数符号确定函数的单调性,属于常用解题技巧.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
8.已知函数f(x)是定义在区间(0,+∞)的可导函数,其导函数为f′(x),且满足xf′(x)>3f(x),则不等式8f(x)>f(2)x3的解集为( )
| A. | {x|x>3} | B. | {x|x>0} | C. | {x|x>2} | D. | {x|0<x>2} |
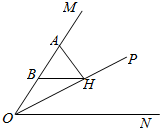 如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.
如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.