题目内容
20.已知等差数列{an}的公差d为整数,且ak=k2+2,a2k=(k+2)2,其中k为常数且k∈N*(1)求k及an
(2)设a1>1,{an}的前n项和为Sn,等比数列{bn}的首项为l,公比为q(q>0),前n项和为Tn,若存在正整数m,使得$\frac{{S}_{2}}{{S}_{m}}={T}_{3}$,求q.
分析 (1)根据等差数列{an}的公差d为整数,且ak=k2+2,a2k=(k+2)2,其中k为常数且k∈N*,
可得a1+(k-1)d=k2+2,a1+(2k-1)d=(k+2)2,解得d=4+$\frac{2}{k}$,即可得出.
(2)由于a1>1,可得an=6n-3,Sn=3n2.而$\frac{{S}_{2}}{{S}_{m}}={T}_{3}$,可得T3=$\frac{4}{{m}^{2}}$=1+q+q2.整理为:q2+q+1-$\frac{4}{{m}^{2}}$=0,利用△≥0,解得m,即可得出.
解答 解:(1)∵等差数列{an}的公差d为整数,且ak=k2+2,a2k=(k+2)2,其中k为常数且k∈N*,
∴a1+(k-1)d=k2+2,a1+(2k-1)d=(k+2)2,解得d=4+$\frac{2}{k}$,∵k=1或2,
∴当k=1时,d=6,a1=3,an=3+6(n-1)=6n-3;
当k=2时,d=5,a1=1,an=1+5(n-1)=5n-4.
(2)∵a1>1,∴an=6n-3,∴Sn=$\frac{n(3+6n-3)}{2}$=3n2.
∵$\frac{{S}_{2}}{{S}_{m}}={T}_{3}$,∴T3=$\frac{12}{3{m}^{2}}$=$\frac{4}{{m}^{2}}$=1+q+q2.
整理为:q2+q+1-$\frac{4}{{m}^{2}}$=0,∵△=1-4$(1-\frac{4}{{m}^{2}})$≥0,解得m2≤$\frac{16}{3}$,∵m∈N*,∴m=1或2.
当m=1时,q2+q-3=0,q>0,解得q=$\frac{\sqrt{13}-1}{2}$.
当m=2时,q2+q=0,q>0,舍去.
综上可得:q=$\frac{\sqrt{13}-1}{2}$.
点评 本题考查了等差数列的通项公式及其前n项和公式、一元二次方程的实数根与判别式的关系、分类讨论方法,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | {x|x>3} | B. | {x|x>0} | C. | {x|x>2} | D. | {x|0<x>2} |
| A. | 经过坐标原点 | B. | 与x轴相交,但与y轴不相交 | ||
| C. | 与y轴相交,但与x轴不相交 | D. | 不经过坐标原点,但与x轴、y轴相交 |
| A. | $\frac{x^2}{4}+y{\;}^2=1$ | B. | x2+y2=4 | C. | $\frac{x^2}{16}+\frac{y^2}{4}=1$ | D. | $\frac{y^2}{16}+\frac{x^2}{4}=1$ |
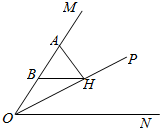 如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.
如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.