题目内容
4.数列{an}中,已知a0=1,a1=3,且${a}_{n}^{2}$-an-1an+1=(-1)n(n∈N),则a3等于33.分析 由递推公式先求出a2,再由递推思想能求出a3.
解答 解:∵数列{an}中,已知a0=1,a1=3,
且${a}_{n}^{2}$-an-1an+1=(-1)n(n∈N),
∴32-1×a2=-1,解得a2=10,
∴102-3×a3=1,解得a3=33,
∴a3等于33.
故答案为:33.
点评 本题考查数列中a3的求法,是基础题,解题时要认真审题,注意递推思想的合理运用.

练习册系列答案
相关题目
13.若实数x、y满足约束条件$\left\{\begin{array}{l}{2x-y-2≤0}\\{2x+y-4≥0}\\{y≤2}\end{array}\right.$,则$\frac{x}{y}$的取值范围是( )
| A. | [$\frac{2}{3}$,2] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,2] | D. | [1,2] |
3.已知集合A={1,m2},B={0,4},则“m=-2”是“A∩B={4}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,定义在[-1,2]上的函数f(x)的图象为折线ACB,则不等式f(x)≤log2(x+1)的解集是[1,2].
如图,定义在[-1,2]上的函数f(x)的图象为折线ACB,则不等式f(x)≤log2(x+1)的解集是[1,2].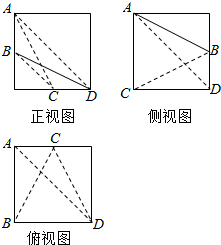 已知,棱长为2的正方体内有一内接四面体A-BCD,且B,C分别为正方体某两条棱的中点,其三视图如图所示:
已知,棱长为2的正方体内有一内接四面体A-BCD,且B,C分别为正方体某两条棱的中点,其三视图如图所示: