题目内容
P是抛物线y2=6x上的点,若P到点(
,0)的距离为15,则P到直线2x+5=0的距离是 .
| 3 |
| 2 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:判断(
,0)是抛物线的焦点坐标,转化题目为抛物线的定义,求解即可.
| 3 |
| 2 |
解答:
解:抛物线y2=6x的焦点坐标为:(
,0),P到点(
,0)的距离为15,
由抛物线的定义可知:P到抛物线的准线方程x=-
的距离为15,x=-
与x=-
到距离为1,
则P到直线2x+5=0的距离是:15+1=16.
故答案为:16.
| 3 |
| 2 |
| 3 |
| 2 |
由抛物线的定义可知:P到抛物线的准线方程x=-
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
则P到直线2x+5=0的距离是:15+1=16.
故答案为:16.
点评:本题考查抛物线的定义与抛物线的性质的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设(x-1)31(2x-1)1981=a0+a1x+a2x2+a3x3+…+a2012x2012,求:
(1)a1+a2+a3+…+a2012;
(2)a0+a1+2a2+3a3+…+2012a2012.
(1)a1+a2+a3+…+a2012;
(2)a0+a1+2a2+3a3+…+2012a2012.
若sin(180°+α)+cos(90°+α)=-a,则cos(270°-α)+2sin(360°-α)的值是( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
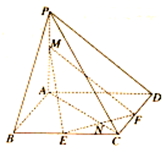 如图,已知在底面为正方形是四棱锥P-ABCD中,PA⊥底面ABCD,M为线段PA
如图,已知在底面为正方形是四棱锥P-ABCD中,PA⊥底面ABCD,M为线段PA