题目内容
在△ABC中,acosA+bcosB=ccosC,试判断三角形的形状.
考点:三角形的形状判断
专题:解三角形
分析:利用正弦定理,和差化积公式可得cos(A-B)=cosC,A=B+C,或B=A+C,再由三角形内角和公式可得A=
,或B=
,即可得答案.
| π |
| 2 |
| π |
| 2 |
解答:
解:在△ABC中,若acosA+bcosB=ccosC,
则sinAcosA+sinBcosB=sinCcosC,
∴sin2A+sin2B=sin2C,2sin(A+B)cos(A-B)=2sinCcosC,
∴cos(A-B)=cosC,
∴A-B=C,或B-A=C,即A=B+C,或B=A+C.
再根据A+B+C=π,可得A=
,或B=
,故△ABC的形状是直角三角形.
则sinAcosA+sinBcosB=sinCcosC,
∴sin2A+sin2B=sin2C,2sin(A+B)cos(A-B)=2sinCcosC,
∴cos(A-B)=cosC,
∴A-B=C,或B-A=C,即A=B+C,或B=A+C.
再根据A+B+C=π,可得A=
| π |
| 2 |
| π |
| 2 |
点评:本题主要考查了正弦定理,和差化积公式的应用,考查了三角形内角和定理的应用,熟练应用相关公式是解题的关键,属于基本知识的考查.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
设(x-1)31(2x-1)1981=a0+a1x+a2x2+a3x3+…+a2012x2012,求:
(1)a1+a2+a3+…+a2012;
(2)a0+a1+2a2+3a3+…+2012a2012.
(1)a1+a2+a3+…+a2012;
(2)a0+a1+2a2+3a3+…+2012a2012.
若sin(180°+α)+cos(90°+α)=-a,则cos(270°-α)+2sin(360°-α)的值是( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
设sinα>0,cosα<0,且sin
>cos
,则
的取值范围是( )
| α |
| 3 |
| α |
| 3 |
| α |
| 3 |
A、(2kπ+
| ||||||||
B、(
| ||||||||
C、(2kπ+
| ||||||||
D、(2kπ+
|
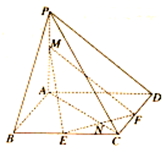 如图,已知在底面为正方形是四棱锥P-ABCD中,PA⊥底面ABCD,M为线段PA
如图,已知在底面为正方形是四棱锥P-ABCD中,PA⊥底面ABCD,M为线段PA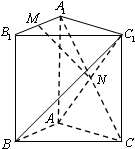 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1,M是A1B1的中点,N是AC1与A1C的交点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1,M是A1B1的中点,N是AC1与A1C的交点.