Question

13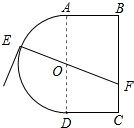．一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成，AB=1米，如图所示，小球从A点出发以大小为5v的速度沿半圆O轨道滚到某点E处，经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内，落点记为F，设∠AOE=θ弧度，小球从A到F所需时间为T．
（1）试将T表示为θ的函数T（θ），并写出定义域；
（2）求时间T最短时θ的值．

Answer 1

分析 （1）通过过点O作OG⊥BC于G，利用OG=1、OF=$\frac{1}{sinθ}$、EF=1+$\frac{1}{sinθ}$、AE=θ及时间、路程与速度之间的关系即得结论；
（2）通过（1）求导可知T′（θ）=-$\frac{（2cosθ+3）（3cosθ-2）}{30vsi{n}^{2}θ}$，进而集合函数的单调性即得结论．

解答 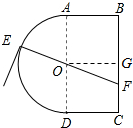解：（1）过点O作OG⊥BC于G，则OG=1，
OF=$\frac{OG}{sinθ}$=$\frac{1}{sinθ}$，EF=1+$\frac{1}{sinθ}$，AE=θ，
∴T（θ）=$\frac{AE}{5v}$+$\frac{EF}{6v}$=$\frac{θ}{5v}$+$\frac{1}{6vsinθ}$+$\frac{1}{6v}$，θ∈[$\frac{π}{4}$，$\frac{3π}{4}$]；
（2）由（1）可知T′（θ）=$\frac{1}{5v}$-$\frac{cosθ}{6vsi{n}^{2}θ}$=$\frac{6si{n}^{2}θ-5cosθ}{30vsi{n}^{2}θ}$=-$\frac{（2cosθ+3）（3cosθ-2）}{30vsi{n}^{2}θ}$，
记cosθ₀=$\frac{2}{3}$，由θ₀∈[$\frac{π}{4}$，$\frac{3π}{4}$]可知：
当θ∈（$\frac{π}{4}$，θ₀）时T′（θ）＜0，即T（θ）在区间（$\frac{π}{4}$，θ₀）上单调递减，
当θ∈（θ₀，$\frac{3π}{4}$）时T′（θ）＞0，即T（θ）在区间（θ₀，$\frac{3π}{4}$）上单调递增，
∴当cosθ=$\frac{2}{3}$时时间T最短．

点评 本题考查根据实际问题选择函数类型，考查分析问题、解决问题的能力，注意解题方法的积累，属于中档题．