题目内容
估计某一天的白昼时间的小时数D(t)的表达式是D(t)=
sin
(t-79)+12,其中t表示某天的序号,t=0表示1月1日,以此类推,常数k与某地所处的纬度有关.在波斯顿,k=6.(结果四舍五入后取整数)
(1)估计从1月1日起多少天后波斯顿的白昼时间最长?多少天后白昼时间最短?
(2)估计在波斯顿一年中有多少天的白昼时间不低于10.5小时.
| k |
| 2 |
| 2π |
| 365 |
(1)估计从1月1日起多少天后波斯顿的白昼时间最长?多少天后白昼时间最短?
(2)估计在波斯顿一年中有多少天的白昼时间不低于10.5小时.
考点:根据实际问题选择函数类型
专题:计算题,应用题,函数的性质及应用
分析:(1)由题意,D(t)=3sin
(t-79)+12,分别令sin
(t-79)=1,sin
(t-79)=-1求解即可.
(2)令D(t)=3sin
(t-79)+12≥10.5;从而求得.
| 2π |
| 365 |
| 2π |
| 365 |
| 2π |
| 365 |
(2)令D(t)=3sin
| 2π |
| 365 |
解答:
解:(1)由题意,D(t)=3sin
(t-79)+12,
令sin
(t-79)=1,
又∵0≤t≤365;
∴t-79=
;
故t=79+
=170.25;
故t=170;
即从1月1日起170天后波斯顿的白昼时间最长,
同理,令sin
(t-79)=-1可解得t=353;
即从1月1日起353天后波斯顿的白昼时间最短;
故估计从1月1日起170天后波斯顿的白昼时间最长,353天后白昼时间最短.
(2)由题意,D(t)=3sin
(t-79)+12≥10.5;
即sin
(t-79)≥-
;
故-
≤
(t-79)≤
;
解得,79-
≤t≤79+
;
故48≤t≤292;
故292-48+1=245天;
估计在波斯顿一年中有245天的白昼时间不低于10.5小时.
| 2π |
| 365 |
令sin
| 2π |
| 365 |
又∵0≤t≤365;
∴t-79=
| 365 |
| 4 |
故t=79+
| 365 |
| 4 |
故t=170;
即从1月1日起170天后波斯顿的白昼时间最长,
同理,令sin
| 2π |
| 365 |
即从1月1日起353天后波斯顿的白昼时间最短;
故估计从1月1日起170天后波斯顿的白昼时间最长,353天后白昼时间最短.
(2)由题意,D(t)=3sin
| 2π |
| 365 |
即sin
| 2π |
| 365 |
| 1 |
| 2 |
故-
| π |
| 6 |
| 2π |
| 365 |
| 7π |
| 6 |
解得,79-
| 365 |
| 12 |
| 7×365 |
| 12 |
故48≤t≤292;
故292-48+1=245天;
估计在波斯顿一年中有245天的白昼时间不低于10.5小时.
点评:本题考查了函数模型在实际问题中的应用,属于中档题.

练习册系列答案
相关题目
方程(
)x=|log
x|的实根的个数为( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
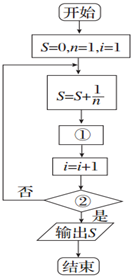 如图给出的是计算1+
如图给出的是计算1+| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 9 |
| A、n=n+2,i>5? |
| B、n=n+2,i=5? |
| C、n=n+1,i=5? |
| D、n=n+1,i>5? |
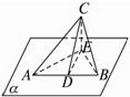 Rt△ABC的斜边AB在平面α内,AC和BC与a所成的角分别为30°与45°,CD是斜边上的高,求CD与平面α所成的角.
Rt△ABC的斜边AB在平面α内,AC和BC与a所成的角分别为30°与45°,CD是斜边上的高,求CD与平面α所成的角.