题目内容
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,点E为PA中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,点E为PA中点. (Ⅰ)求证:DE∥平面PBC;
(Ⅱ)求证:平面PBC⊥平面PAB;
(Ⅲ)若∠PDA=
| π |
| 4 |
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)取PB中点F,连结EF,CF,由已知条件推导出四边形EFCD是平行四边形,由此能证明DE∥平面PBC.
(Ⅱ)由线面垂直得PA⊥BC,再由AB⊥BC,得BC⊥平面PAB,由此能证明平面PBC⊥平面PAB.
(Ⅲ)求出棱锥的高,即可求四棱锥P-ABCD的体积.
(Ⅱ)由线面垂直得PA⊥BC,再由AB⊥BC,得BC⊥平面PAB,由此能证明平面PBC⊥平面PAB.
(Ⅲ)求出棱锥的高,即可求四棱锥P-ABCD的体积.
解答:
(Ⅰ)证明:取PB中点F,连结EF,CF,
∵E是PA中点,∴EF平行且等于
AB,
∵AB∥CD,AB=2BC=2CD=2,
∴EF平行且等于CD,∴四边形EFCD是平行四边形,
∴DE∥CF,
∵DE不包含于平面PBC,CF?平面PBC,
∴DE∥平面PBC.
(Ⅱ)证明:∵PA⊥底面ABCD,BC?底面ABCD,
∴PA⊥BC,
∵AB⊥BC,PA∩AB=A,∴BC⊥平面PAB,
∵BC?平面PBC,∴平面PBC⊥平面PAB.
(Ⅲ)解:∵ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,
∴AD=
,
∵PA⊥底面ABCD,∠PDA=
,
∴PA=
,
∴四棱锥P-ABCD的体积为
×
×(1+2)×1×
=
.
∵E是PA中点,∴EF平行且等于
| 1 |
| 2 |
∵AB∥CD,AB=2BC=2CD=2,
∴EF平行且等于CD,∴四边形EFCD是平行四边形,
∴DE∥CF,
∵DE不包含于平面PBC,CF?平面PBC,
∴DE∥平面PBC.
(Ⅱ)证明:∵PA⊥底面ABCD,BC?底面ABCD,
∴PA⊥BC,
∵AB⊥BC,PA∩AB=A,∴BC⊥平面PAB,
∵BC?平面PBC,∴平面PBC⊥平面PAB.
(Ⅲ)解:∵ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,
∴AD=
| 2 |
∵PA⊥底面ABCD,∠PDA=
| π |
| 4 |
∴PA=
| 2 |
∴四棱锥P-ABCD的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,考查锥体体积的求法,属于中档题.

练习册系列答案
相关题目
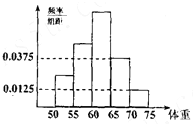 为了了解某市今年准备报考体育专业的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,则第2小组的频率为
为了了解某市今年准备报考体育专业的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,则第2小组的频率为