题目内容
某商品每件成本10元,售价为30元,每星期卖出100件.如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值x(单位:元,0≤x≤30)成正比.已知商品单价降低2元时,一星期多卖出20件.
(1)将一个星期的商品销售利润y表示成x的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
(1)将一个星期的商品销售利润y表示成x的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)先设商品降价x元,写出多卖的商品数,则可计算出商品在一个星期的获利数,再依题意:“商品单价降低2元时,一星期多卖出20件”求出比例系数即可得一个星期的商品销售利润表示成x的函数;
(2)根据(1)中得到的函数,利用配方法得出以定价为多少元时,能使一个星期的商品销售利润最大.
(2)根据(1)中得到的函数,利用配方法得出以定价为多少元时,能使一个星期的商品销售利润最大.
解答:
解:(1)设商品降价x元,则每个星期多卖的商品数为kx,
则依题意有y=(30-x-10)(100+kx)=(20-x)(100+kx)
又由已知条件知20=2k,于是有k=10,
所以y=(20-x)(100+10x),0≤x≤30.
(2)根据(1)知y=(20-x)(100+10x)=10(-x2+10x+200)=-10(x-5)2+2250
所以当x=5时,销售利润最大,最大值为2250元.
所以定价为30-5=25元时,能使一个星期的商品销售利润最大.
则依题意有y=(30-x-10)(100+kx)=(20-x)(100+kx)
又由已知条件知20=2k,于是有k=10,
所以y=(20-x)(100+10x),0≤x≤30.
(2)根据(1)知y=(20-x)(100+10x)=10(-x2+10x+200)=-10(x-5)2+2250
所以当x=5时,销售利润最大,最大值为2250元.
所以定价为30-5=25元时,能使一个星期的商品销售利润最大.
点评:本小题主要考查根据实际问题建立数学模型,以及运用函数的知识解决实际问题的能力.

练习册系列答案
相关题目
 如图,在棱长为1的正方体ABCD-A1B1C1D1中.
如图,在棱长为1的正方体ABCD-A1B1C1D1中. 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.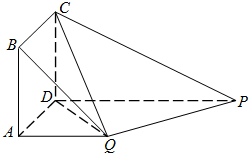 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=