题目内容

7．已知f（x）是定义在（0，+∞）上的非负可导函数，且满足xf'（x）+f（x）≤0，对任意的0＜a＜b，则必有（　　）
A．af（b）≤bf（a）B．bf（a）≤af（b）C．af（a）≤f（b）D．bf（b）≤f（a）

分析 先构造函数，再由导数与原函数的单调性的关系解决．

解答 解：xf′（x）+f（x）≤0⇒[xf（x）]′≤0⇒函数F（x）=xf（x）在（0，+∞）上为常函数或递减，
又0＜a＜b且f（x）非负，于是有：af（a）≥bf（b）≥0①$\frac{1}{{a}^{2}}$＞$\frac{1}{{b}^{2}}$＞0②，
①②两式相乘得：$\frac{f（a）}{a}$≥$\frac{f（b）}{b}$≥0⇒af（b）≤bf（a），
故选：A．

点评 本题的难点在对不等式②的设计，需要经验更需要灵感．

练习册系列答案
相关题目
10．函数f（x）=-x3+ax2-x-1在R上不单调，则实数a的取值范围是（　　）
A．（-∞，-$\sqrt{3}$]∪[$\sqrt{3}$，+∞）B．（-∞，-$\sqrt{3}$）∪（$\sqrt{3}$，+∞）C．[-$\sqrt{3}$，$\sqrt{3}$]D．（-$\sqrt{3}$，$\sqrt{3}$）
18．已知函数f（x）=-sinx+ax（a为常数）．
（1）若x∈[0，$\frac{π}{2}$]时函数f（x）单调递增，求实数a的取值范围；
（2）证明：当x∈[0，$\frac{π}{2}$]时，cosx≥-$\frac{1}{2}$x2+1．
15．函数y=（x2-1）2+2的极值点是（　　）
A．x=1B．x=-1或0C．x=-1或1或0D．x=0或1
2．定义在R上的偶函数f（x）满足f（2-x）=f（x），且在[-3，-2]上是减函数，α，β是锐角三角形的两个内角，下列不等式正确的是（　　）
A．f（sinα）＞f（cosβ）B．f（sinα）＜f（cosβ）C．f（cosα）＜f（cosβ）D．f（sinα）＞f（sinβ）
12．在平面直角坐标系中，已知角α的终边经过点P（-3，4）
（1）求sinα和cosα的值；
（2）化简并求值：$\frac{{sin（2π-α）cos（π+α）cos（\frac{π}{2}+α）cos（\frac{11π}{2}-α）}}{{cos（π-α）sin（3π-α）sin（-π-α）sin（\frac{9π}{2}+α）}}$．
19．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的体积为（　　）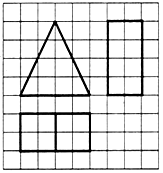
A．16B．$\frac{16}{3}$C．32D．48
16．设曲线y=3x-ln（x+1）在点（0，0）处的切线方程2x-y=0．
17．已知向量$\overrightarrow{a}$=（4，3），$\overrightarrow{b}$=（-1，2）．
（1）求|$\overrightarrow{a}-\overrightarrow{b}$|；
（2）若向量$\overrightarrow{a}-λ\overrightarrow{b}$与2$\overrightarrow{a}+\overrightarrow{b}$平行，求λ的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网