题目内容
一个口袋内有大小、形状相同的6个白球和5个黑球,从中随机取出3个球,则至少取到2个白球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:排列、组合及简单计数问题
专题:概率与统计
分析:先求从中随机取出3个球,没有限制条件的3个有
种,至少取到2个白球分两种情况,两个和三个,代入古典概型公式,即可得到答案.
| C | 3 11 |
解答:
解:从中随机取出3个球,没有限制条件的3个有
种,至少取到2个白球分两种情况,两个和三个有
•
种,
根据古典概率公式得至少取到2个白球的概率P=
=
.
故选:D.
| C | 3 11 |
| C | 2 6 |
| C | 1 5 |
| +C | 3 6 |
根据古典概率公式得至少取到2个白球的概率P=
| ||||||
|
| 19 |
| 33 |
故选:D.
点评:本题考查的知识点是古典概型,其中计算出所有取法的基本事件总数,及两个球中至少有一个白球的基本事件个数,是解答本题的关键.

练习册系列答案
相关题目
函数满足f(1)=1,且f(x)在R上的导数f′(x)>
,则不等式f(lnx)-
lnx<
的解集为( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、(0,1) |
| B、(0,e) |
| C、(1,+∞) |
| D、(e,+∞) |
在长方体ABCD-A1B1C1D1中,AB=2,BC=2,DD1=3,则AC与BD1所成角的余弦值为( )
| A、0 | ||||
B、
| ||||
C、-
| ||||
D、
|
将一枚骰子连续抛掷两次,则向上点数之差的绝对值不大于3的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
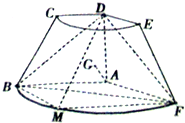 如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧
如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧
 如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=
如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=