题目内容
已知
=(1-t,1-t,t),
=(2,t,t),则|
-
|的最小值是( )
| a |
| b |
| b |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:空间向量运算的坐标表示
专题:空间向量及应用
分析:由已知得
-
=(1+t,2t-1,0),从而|
-
|=
,由此利用配方法能求出|
-
|的最小值.
| b |
| a |
| b |
| a |
| (1+t)2+(2t-1)2 |
| b |
| a |
解答:
解:∵
=(1-t,1-t,t),
=(2,t,t),
∴
-
=(1+t,2t-1,0),
∴|
-
|=
=
=
,
∴当t=
时,|
-
|的最小值是
.
故选:C.
| a |
| b |
∴
| b |
| a |
∴|
| b |
| a |
| (1+t)2+(2t-1)2 |
| 5t2-2t+2 |
5(t-
|
∴当t=
| 1 |
| 5 |
| b |
| a |
3
| ||
| 5 |
故选:C.
点评:本题考查向量的模的最小值的求法,是基础题,解题时要认真审题,注意配方法的合理运用.

练习册系列答案
相关题目
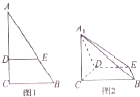 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到A1DE的位置,使A2C⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到A1DE的位置,使A2C⊥CD,如图2.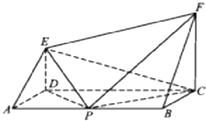 如图,ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC=CF=2a,p为AB的中点.
如图,ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC=CF=2a,p为AB的中点.