题目内容
设f(x)=x2-2x+2m,当x∈[-1,+∞)时,f(x)≥m恒成立,求m的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:将不等式恒成立转化为求二次函数的最值即可求出m的取值范围.
解答:
解:当x∈[-1,+∞)时,f(x)≥m恒成立,
得到x2-2x+2m≥m,
即m≥-x2+2x=-(x-1)2+1,
设g(x)=-(x-1)2+1,
∵当x∈[-1,+∞)时,
g(x)≤1,
∴m≥1,
即m的取值范围是m≥1.
得到x2-2x+2m≥m,
即m≥-x2+2x=-(x-1)2+1,
设g(x)=-(x-1)2+1,
∵当x∈[-1,+∞)时,
g(x)≤1,
∴m≥1,
即m的取值范围是m≥1.
点评:本题主要考查不等式恒成立问题,将不等式转化为一元二次不等式,利用不等式求函数的最值是解决本题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
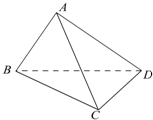 在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.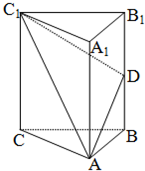 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中,