题目内容
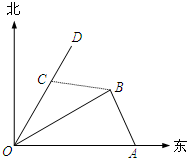 如图,港口A在港口O的正东120海里处,小岛B在港口O的北偏东60°的方向,且在港口A北偏西30°的方向上.一艘科学考察船从港口O出发,沿北偏东30°的OD方向以20海里/小时的速度驶离港口O.一艘给养快艇从港口A以60海里/小时的速度驶向小岛B,在B岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
如图,港口A在港口O的正东120海里处,小岛B在港口O的北偏东60°的方向,且在港口A北偏西30°的方向上.一艘科学考察船从港口O出发,沿北偏东30°的OD方向以20海里/小时的速度驶离港口O.一艘给养快艇从港口A以60海里/小时的速度驶向小岛B,在B岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.(1)求给养快艇从港口A到小岛B的航行时间;
(2)给养快艇驶离港口A后,最少经过多少时间能和科考船相遇?
考点:解三角形的实际应用
专题:应用题,解三角形
分析:(1)给养快艇从港口A到小岛B的航行时间,已知其速度,则只要求得AB的路程,再利用路程公式即可求得所需的时间.
(2)由(1)知,给养快艇从港口A驶离2小时后,从小岛B出发与科考船汇合,根据题意确定各边长和各角的值,然后由余弦定理解决问题.
(2)由(1)知,给养快艇从港口A驶离2小时后,从小岛B出发与科考船汇合,根据题意确定各边长和各角的值,然后由余弦定理解决问题.
解答:
解:(1)由题意知,在△OAB中,OA=120,∠AOB=30°,∠OAB=60°.
于是AB=60,而快艇的速度为60海里/小时,
所以快艇从港口A到小岛B的航行时间为1小时. …(5分)
(2)由(1)知,给养快艇从港口A驶离2小时后,从小岛B出发与科考船汇合.
为使航行的时间最少,快艇从小岛B驶离后必须按直线方向航行,
设t小时后恰与科考船在C处相遇.…(7分)
在△OAB中,OA=120,∠AOB=30°,∠OAB=60°,所以OB=60
,
而在△OCB中,BC=60t,OC=20(2+t),∠BOC=30°,…(9分)
由余弦定理,得BC2=OB2+OC2-2OB•OC•cos∠BOC,
即(60t)2=(60
)2+[20(2+t)]2-2×60
×20(2+t)×
,
亦即8t2+5t-13=0,解得t=1或t=-
(舍去).…(12分)
故t+2=3.即给养快艇驶离港口A后,最少经过3小时能和科考船相遇.…(14分)
于是AB=60,而快艇的速度为60海里/小时,
所以快艇从港口A到小岛B的航行时间为1小时. …(5分)
(2)由(1)知,给养快艇从港口A驶离2小时后,从小岛B出发与科考船汇合.
为使航行的时间最少,快艇从小岛B驶离后必须按直线方向航行,
设t小时后恰与科考船在C处相遇.…(7分)
在△OAB中,OA=120,∠AOB=30°,∠OAB=60°,所以OB=60
| 3 |
而在△OCB中,BC=60t,OC=20(2+t),∠BOC=30°,…(9分)
由余弦定理,得BC2=OB2+OC2-2OB•OC•cos∠BOC,
即(60t)2=(60
| 3 |
| 3 |
| ||
| 2 |
亦即8t2+5t-13=0,解得t=1或t=-
| 13 |
| 8 |
故t+2=3.即给养快艇驶离港口A后,最少经过3小时能和科考船相遇.…(14分)
点评:本题主要考查余弦定理的应用,考查学生分析解决问题的能力.余弦定理在解实际问题时有着广泛的应用,一定要熟练的掌握.

练习册系列答案
相关题目
下列说法正确的是( )
| A、函数的极大值大于函数的极小值 |
| B、若f′(x0)=0,则x0为函数f(x)的极值点 |
| C、函数的最值一定是极值 |
| D、在闭区间上的连续函数一定存在最值 |
 如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,AC=2,D是AC的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,AC=2,D是AC的中点. 如图,斜三棱柱ABC-A1B1C1的侧棱长为
如图,斜三棱柱ABC-A1B1C1的侧棱长为 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中,