题目内容
函数f（x）=x+
的值域 ．
| 4 |
| x-1 |
考点：函数的值域
专题：转化思想,函数的性质及应用
分析：利用换元思想把函数f（x）转化为g（t）=t+
+1，t∈（-∞，0）∪（0，+∞）
再根据函数的单调性求解函数的值域．
| 4 |
| t |
再根据函数的单调性求解函数的值域．
解答：
解：设t=x-1，x=t+1，函数f（x）=x+
，可以得到g（t）=t+
+1，t∈（-∞，0）∪（0，+∞）
根据g（x）图象，结合均值不等式可判断函数在区间（-∞，-1），（1，+∞）上为增函数，在（-1，0），（0，+1）上为函数减，
g（1）=6，g（-1）；=-4，
故答案为：（-∞，-4]∪[6，+∞）
| 4 |
| x-1 |
| 4 |
| t |
根据g（x）图象，结合均值不等式可判断函数在区间（-∞，-1），（1，+∞）上为增函数，在（-1，0），（0，+1）上为函数减，
g（1）=6，g（-1）；=-4，
故答案为：（-∞，-4]∪[6，+∞）
点评：本题考查了换元思想，以及对勾函数的单调性判断在求最值，函数解析式比较简单，很容易画图象．
练习册系列答案
相关题目
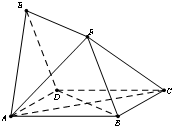如图，四边形ABCD与BDEF均为菱形，∠DAB=∠DBF=60，且FA=FC．
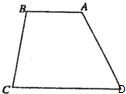如图所示，有一块四边形的空、地，现欲把它绿化，需知道其面积，以便估算费用．现测得AB=5m，AD=CD=19m，BC=16m，∠ADC=60°．则这块四边形空地的面积是
如图是函数y=f（x）的导函数f′（x）的图象，对下列四个命题：其中正确的命题是