题目内容
 在函数f(x)=1gx的图象上有三点A、B、C,横坐标依次是m-1,m,m+1(m>2).
在函数f(x)=1gx的图象上有三点A、B、C,横坐标依次是m-1,m,m+1(m>2).(1)试比较f(m-1)+f(m+1)与2f(m)的大小;
(2)解不等式f(x)>f(x2+x-2)
(3)求△ABC的面积S=g(m)的值域.
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:(1)根据f(x)=1gx具体表示出来,运用对数的性质比较,
(2)转化为
,求解即可.
(3)根据图形列出式子,转化为对数函数,运用单调性求解.
(2)转化为
|
(3)根据图形列出式子,转化为对数函数,运用单调性求解.
解答:
解:(1)∵f(m-1)+f(m+1)=lg(m-1)+lg(m+1)=lg(m2-1),
2f(m)=lgm2>lg(m2-1),
∴f(m-1)+f(m+1)<2f(m)
(2)由题意f(x)>f(x2+x-2),f(x)=1gx
知,
,解得1<x<
所以不等式的解集是{x|1<x<
}
(3)S=g(m)=S A1ABB1+S B1BCC1-SCAA1C1
S=
[lg(m-1)+lgm]+
[lg(m+1)+lgm]-
[lg(m-1)+lg(m+1)]×2
S=
lg
=
lg
S=
lg(1+
),
因m>2时,单调递减.
所以g(m)>g(2)=lg2-
lg3,
故△ABC的面积S=g(m)的值域为:(lg2-
lg3,+∞)
2f(m)=lgm2>lg(m2-1),
∴f(m-1)+f(m+1)<2f(m)
(2)由题意f(x)>f(x2+x-2),f(x)=1gx
知,
|
| 2 |
所以不等式的解集是{x|1<x<
| 2 |
(3)S=g(m)=S A1ABB1+S B1BCC1-SCAA1C1
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S=
| 1 |
| 2 |
| m2 |
| (m+1)(m-1) |
| 1 |
| 2 |
| m2 |
| m2-1 |
S=
| 1 |
| 2 |
| 1 |
| m2-1 |
因m>2时,单调递减.
所以g(m)>g(2)=lg2-
| 1 |
| 2 |
故△ABC的面积S=g(m)的值域为:(lg2-
| 1 |
| 2 |
点评:本题考察了对数函数的概念,性质,以及运算等问题,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
不等式|y|≤x表示的平面区域为( )
A、 |
B、 |
C、 |
D、 |
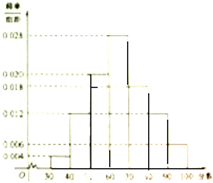 某校高一年级共有800名学生,其中男生480名,女生320名,在某次满分为100分的数学考试中,所有学生成绩在30分及30分以上,成绩在“80分及80分以上”的学生视为优秀.现按性别采用分层抽样的方法共抽取100名学生,将他们的成绩按[30,40]、[40,50]、[50,60]、[60,70]、[70,80]、[80,90]、[90,100]分成七组.得到的频率分布直方图如图所示:
某校高一年级共有800名学生,其中男生480名,女生320名,在某次满分为100分的数学考试中,所有学生成绩在30分及30分以上,成绩在“80分及80分以上”的学生视为优秀.现按性别采用分层抽样的方法共抽取100名学生,将他们的成绩按[30,40]、[40,50]、[50,60]、[60,70]、[70,80]、[80,90]、[90,100]分成七组.得到的频率分布直方图如图所示: 如图所示,⊙O的两条切线PA和PB相交于点P,与⊙O相切于A,B两点,C是⊙O上的一点,若∠P=70°,则∠ACB=
如图所示,⊙O的两条切线PA和PB相交于点P,与⊙O相切于A,B两点,C是⊙O上的一点,若∠P=70°,则∠ACB=