题目内容
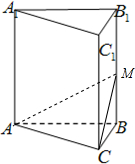
已知直三棱柱ABC-A1B1C1中,∠ABC=90°,AC=AA1=2
,AB=2,M为BB1的中点,则B1与平面ACM的距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:根据M为BB1的中点,可得B1与平面ACM的距离等于B与平面ACM的距离,由等体积可计算B与平面ACM的距离.
解答:
 解:∵M为BB1的中点,
解:∵M为BB1的中点,
∴B1与平面ACM的距离等于B与平面ACM的距离,
∵,∠ABC=90°,AC=2
,AB=2,
∴BC=2,
∵AA1=2
,M为BB1的中点,
∴AM=BM=
,
∴AC边上的高为2,
∴S△MAC=
•2
•2=2
,S△ABC=
•2•2=2,
设B与平面ACM的距离为h,则
由等体积可得
•2•
=
•2
•h,
∴h=1.
故选:D.
 解:∵M为BB1的中点,
解:∵M为BB1的中点,∴B1与平面ACM的距离等于B与平面ACM的距离,
∵,∠ABC=90°,AC=2
| 2 |
∴BC=2,
∵AA1=2
| 2 |
∴AM=BM=
| 6 |
∴AC边上的高为2,
∴S△MAC=
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
设B与平面ACM的距离为h,则
由等体积可得
| 1 |
| 3 |
| 2 |
| 1 |
| 3 |
| 2 |
∴h=1.
故选:D.
点评:本题考查点、线、面间的距离计算,考查体积计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
设函数f(x)=mx2+mx+m-1,若不等式f(x)≥0解集为空集,则实数m的取值范围为( )
| A、(-∞,0] | ||
B、(-∞,0)∪(
| ||
| C、(-∞,0) | ||
D、(-∞,0)∪(
|
一个学生能够通过某种英语听力测试的概率是
,他连续测试2次,那么其中恰有一次获得通过的概率是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题中正确的是( )
| A、若直线m∥平面α,直线n?α,则m∥n |
| B、若直线m⊥平面α,直线n?α,则m⊥n |
| C、若平面α∥平面β,直线m?α,直线n?β,则m∥n |
| D、若平面α⊥平面β,直线m?α,则m⊥β |
若sinα=
,且α∈[
,π],则α可以表示成( )
| 1 |
| 5 |
| π |
| 2 |
A、
| ||||
B、
| ||||
C、π-arcsin
| ||||
D、π+arcsin
|
用数字0、1、2、3能组成多少个没有重复数字的四位偶数( )
| A、6 | B、10 | C、12 | D、24 |
若(
+
)n的展开式中,各项系数的和与各项二项式系数的和之比为64,则n=( )
| x |
| 3 |
| x |
| A、4 | B、5 | C、6 | D、7 |