题目内容
如图，AB为⊙O的直径过点B作⊙O的切线BC，OC交⊙O于点E，AE的延长线交BC于点D，若AB=BC=2，则CD的长为考点：与圆有关的比例线段
专题：选作题,立体几何
分析：证明△CED∽△CBE，利用弦切角的知识证明CE2=CD•CB，在Rt三△OBC中，利用勾股定理即可得出CE的长，利用CE2=CD•CB，代入CE即可得出CD的长．
解答：
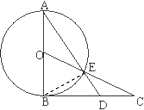解：连接BE．
∵BC为⊙O的切线∴∠ABC=90°
∵AB为⊙O的直径∴∠AEB=90°
∴∠DBE+∠OBE=90°，∠AEO+∠OEB=90°
∵OB=OE，∴∠OBE=∠OEB∴∠DBE=∠AEO
∵∠AEO=∠CED∴∠CED=∠CBE，
∵∠C=∠C，∴△CED∽△CBE，
∴CE2=CD•CB
∵OB=1，BC=2，∴OC=
，∴CE=OC-OE=
-1
（
-1）2=2CD，∴CD=3-
．
故答案为：3-
解：连接BE．∵BC为⊙O的切线∴∠ABC=90°
∵AB为⊙O的直径∴∠AEB=90°
∴∠DBE+∠OBE=90°，∠AEO+∠OEB=90°
∵OB=OE，∴∠OBE=∠OEB∴∠DBE=∠AEO
∵∠AEO=∠CED∴∠CED=∠CBE，
∵∠C=∠C，∴△CED∽△CBE，
∴CE2=CD•CB
∵OB=1，BC=2，∴OC=
| 5 |
| 5 |
（
| 5 |
| 5 |
故答案为：3-
| 5 |
点评：本题主要考查了切线的性质及其应用，同时考查了相似三角形的判定和解直角三角形等知识点，运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
相关题目