题目内容
已知arg(z+1)=
,arg(z-1)=-
π,求z的幅角.
| π |
| 3 |
| 5 |
| 6 |
考点:复数的基本概念
专题:数系的扩充和复数
分析:设z=a+bi,(a,b∈R).∴z+1=a+1+bi,z-1=a-1+bi.由于arg(z+1)=
,arg(z-1)=-
π,可得
,解得a,b.即可得出z的幅角.
| π |
| 3 |
| 5 |
| 6 |
|
解答:
解:设z=a+bi,(a,b∈R).∴z+1=a+1+bi,z-1=a-1+bi.
∵arg(z+1)=
,arg(z-1)=-
π,
∴
,解得a=-2,b=-
.
∴z=-2-
i
∴z的幅角=π+arctan
.
∵arg(z+1)=
| π |
| 3 |
| 5 |
| 6 |
∴
|
| 3 |
∴z=-2-
| 3 |
∴z的幅角=π+arctan
| ||
| 2 |
点评:本题考查了复数的幅角的求法,属于基础题.

练习册系列答案
相关题目
已知数列1,a1,a2,9成等差数列,1,b1,b2,b3,9成等比数列,则
=( )
| a1+a2 |
| b2 |
| A、3 | ||
| B、-3 | ||
C、
| ||
D、±
|
已知集合A={-1,0,1,2},B={x|ln(x-1)=0},则A∩B=( )
| A、{-1} | B、{0} |
| C、{1} | D、{2} |
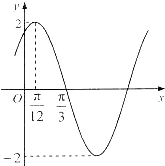
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<
)的部分图象如图所示,则( )
| π |
| 2 |

A、ω=2,φ=
| ||||
B、ω=
| ||||
C、ω=2,φ=
| ||||
D、ω=
|
 在以O为直角顶点的直角三角形OAB的外侧作两个正方形OAPQ和OBRS,设QS的中点为M(本题所有的点均在同一个平面内,如图所示),取直角的两边为坐标轴,试证明:
在以O为直角顶点的直角三角形OAB的外侧作两个正方形OAPQ和OBRS,设QS的中点为M(本题所有的点均在同一个平面内,如图所示),取直角的两边为坐标轴,试证明: