题目内容
朝露润物新苗壮,四中学子读书忙.天蒙蒙亮,值日老师站在边长为100米的正方形运动场正中间,环顾四周.但老师视力不好,只能看清周围10米内的同学.郑鲁力同学随机站在运动场上朗读.郑鲁力同学被该老师看清的概率为 .
考点:几何概型
专题:计算题,概率与统计
分析:根据题意,所有的基本事件对应的图形是边长为100米的正方形,而事件“郑鲁力同学被该老师看清”对应的图形是正方形内部且半径等于10米的圆,由此算出相应图形的面积并利用几何概型公式,即可算出所求的概率.
解答:
解:记“郑鲁力同学被该老师看清”为事件A,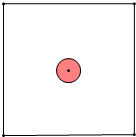
∵值日老师站在边长为100米的正方形运动场正中间,
∴所有的基本事件对应的图形是边长为100米的正方形,
其面积为S=1002=10000m2,
又∵老师只能看清周围10米内的同学,当郑鲁力同学距离正方形中心的距离
不超过10米时,能够被值日老师看清,
∴事件A对应的图形是以正方形中心为圆心、半径r=10米的圆,
其面积为S'=π×102=100πm2,
因此,事件A发生的概率为P(A)=
=
=
.
即郑鲁力同学被该老师看清的概率为
.
故答案为:

∵值日老师站在边长为100米的正方形运动场正中间,
∴所有的基本事件对应的图形是边长为100米的正方形,
其面积为S=1002=10000m2,
又∵老师只能看清周围10米内的同学,当郑鲁力同学距离正方形中心的距离
不超过10米时,能够被值日老师看清,
∴事件A对应的图形是以正方形中心为圆心、半径r=10米的圆,
其面积为S'=π×102=100πm2,
因此,事件A发生的概率为P(A)=
| S′ |
| S |
| 100π |
| 10000 |
| π |
| 100 |
即郑鲁力同学被该老师看清的概率为
| π |
| 100 |
故答案为:
| π |
| 100 |
点评:本题给出几何概率模型,求事件“郑鲁力同学被该老师看清”的概率,着重考查了平面图形面积的计算与几何概率计算公式等知识,属于基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
对任意的实数t,直线ty=x-
与圆x2+y2=1的位置关系一定是( )
| 1 |
| 2 |
| A、相切 |
| B、相交且直线不过圆心 |
| C、相交且直线不一定过圆心 |
| D、相离 |
若动点M到定点F1(0,-1)、F2(0,1)的距离之和为2,则点M的轨迹为( )
| A、椭圆 |
| B、直线F1F2 |
| C、线段F1F2 |
| D、直线F1F2的垂直平分线 |
 从学校参加数学竞赛的学生的试卷中抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘制频率分布直方图如图,从左至右各小组的小长方形的高之比为1:3:6:4:2,最右边一组的频数是6,请结合直方图提供的信息,解答下列问题:
从学校参加数学竞赛的学生的试卷中抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘制频率分布直方图如图,从左至右各小组的小长方形的高之比为1:3:6:4:2,最右边一组的频数是6,请结合直方图提供的信息,解答下列问题: