题目内容
已知抛物线y2=2px(p>0)上一点M到它的准线的距离为2,且M到抛物线顶点的距离等于M到它的焦点的距离,则此抛物线的焦点坐标是 .
考点:抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:设点M(x,y),由已知条件推导出x+
=2,x2+y2=(x-
)2+y2,由此求出x=
,从而能求出焦点坐标为(
,0).
| p |
| 2 |
| p |
| 2 |
| p |
| 4 |
| 4 |
| 3 |
解答:
解:设点M(x,y)到它的准线的距离为2,
则x+
=2,
∵M到此抛物线顶点的距离等于M到它的焦点的距离,
∴x2+y2=(x-
)2+y2,
解得x=
,
+
=2,解得p=
.
∴焦点坐标为(
,0).
故答案为:(
,0).
则x+
| p |
| 2 |
∵M到此抛物线顶点的距离等于M到它的焦点的距离,
∴x2+y2=(x-
| p |
| 2 |
解得x=
| p |
| 4 |
| p |
| 4 |
| p |
| 2 |
| 8 |
| 3 |
∴焦点坐标为(
| 4 |
| 3 |
故答案为:(
| 4 |
| 3 |
点评:本题考查抛物线的标准方程的求法,是中档题,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
设全集为R,集合M={x∈R|f(x)≠0},N={x∈R|g(x)≠0},则集合{x∈R|f(x)•g(x)=0}等于( )
| A、(∁RM)∩(∁RN) |
| B、(∁RM)∪(∁RN) |
| C、M∪(∁RN) |
| D、(∁RM)∪N |
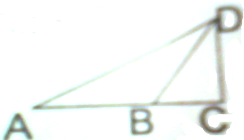 如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100
如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100