已知扇形的周长为10cm.面积为4cm2.求扇形的弧长．题目和参考答案——青夏教育精英家教网—

题目内容

6．已知扇形的周长为10cm，面积为4cm²，求扇形的弧长．

分析利用扇形的周长、面积公式列出方程组，能求出扇形的弧长．

解答解：∵扇形的周长为10cm，面积为4cm²，
∴$\left\{\begin{array}{l}{l+2r=10}\\{\frac{1}{2}lr=4}\end{array}\right.$，解得l=2，r=4，或l=8，r=1（舍），
∴扇形的弧长为2cm．

点评本题考查扇形弧长的求法，是基础题，解题时要认真审题，注意扇形的周长、面积公式的合理运用．

练习册系列答案

17．若直线l与两直线y=1，直线x-y-7=0分别交于M，N两点且MN的中点为P（1，-1），则直线l的斜率等于（　　）

14．已知sin（3π+α）=lg$\frac{1}{\root{3}{10}}$，求$\frac{cos（π+α）}{cosα[cos（π-α）-1]}$+$\frac{cos（α-2π）}{cosαcos（π-α）+cos（-α）}$的值．

1．已知函数为奇函数，且f（$\frac{π}{4}$）=0，其中a∈R，θ∈（0，π），f（x）=（a+2cos²x）cos（2x+θ）．
（1）求a，θ的值；
（2）若f（$\frac{a}{4}$）=-$\frac{2}{5}$，α∈（$\frac{π}{2}$，π），求sin（α+$\frac{π}{3}$）的值．

11．已知函数f（x）=（x-a）²+（e^x-a）²（a∈R），若存在x₀∈R，使得f（x₀）≤$\frac{1}{2}$成立，则实数a的值为（　　）

18．在△ABC中，a²+b²+c²=2$\sqrt{3}$bcsinA，则△ABC的形状是（　　）

8．

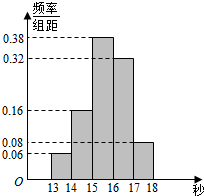某班50名学生在一次百米测试中，成绩全部在13秒与18秒之间，大于或等于14秒的为良好，由测试结果得到的频率分布直方图如图，则该班百米测试中成绩良好的人数有人47．

9．如果f（x）在[-5，5]上是奇函数，且f（3）＜f（1），则（　　）

试题分类