题目内容
5.求证:(1)$\frac{sinα-cosα+1}{sinα+cosα-1}=\frac{1+sinα}{cosα}$;
(2)2(sin6θ+cos6θ)-3(sin4θ+cos4θ)+1=0.
分析 (1)直接利用分析法证明三角恒等式.
(2)利用平方和公式,立方和公式变形化简sin4θ+cos4θ,sin6θ+cos6θ,利用同角三角函数间基本关系化简计算即可得证.
解答 证明:(1)要证$\frac{sinα-cosα+1}{sinα+cosα-1}=\frac{1+sinα}{cosα}$,
需要证cosα(sinα-cosα+1)=(1+sinα)(sinα+cosα-1),
即证sinαcosα-cos2α+cosα=sinα+cosα-1+sin2α+sinαcosα-sinα,
也就是证:sin2α+cos2α=1,此式显然成立.
∴$\frac{sinα-cosα+1}{sinα+cosα-1}=\frac{1+sinα}{cosα}$.
(2)∵sin4θ+cos4θ=(sin2α+cos2α)2-2sin2αcos2α=1-2sin2αcos2α,
∴sin6θ+cos6θ=(sin2α+cos2α)(sin4α+cos4α-sin2αcos2α)=1-3sin2αcos2α,
∴2(sin6θ+cos6θ)-3(sin4θ+cos4θ)+1
=2(1-3sin2αcos2α)-3(1-2sin2αcos2α)+1
=2-6sin2αcos2α-3+6sin2αcos2α+1
=0.
得证.
点评 本题考查了三角恒等式的证明,考查了分析法证明三角恒等式,解题中要注意一些常见式子的变形形式,关键是掌握分析法证题的步骤,属于中档题.

练习册系列答案
相关题目
13.sin2(π+α)-cos(π-α)•cosα+1=( )
| A. | 2 | B. | 1 | C. | 2sin2α | D. | 0 |
17.若直线l与两直线y=1,直线x-y-7=0分别交于M,N两点且MN的中点为P(1,-1),则直线l的斜率等于( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
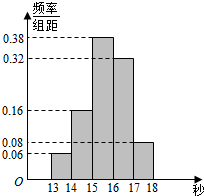 某班50名学生在一次百米测试中,成绩全部在13秒与18秒之间,大于或等于14秒的为良好,由测试结果得到的频率分布直方图如图,则该班百米测试中成绩良好的人数有人47.
某班50名学生在一次百米测试中,成绩全部在13秒与18秒之间,大于或等于14秒的为良好,由测试结果得到的频率分布直方图如图,则该班百米测试中成绩良好的人数有人47.