题目内容
19.一盒中有12个乒乓球,其中9个新的,3个旧的,从盒中任取3个球来用,用完后装回盒中,此时盒中旧球个数X是一个随机变量,求X的分布列及数学期望.分析 由题意知旧球个数X的所有可能取值为3,4,5,6.分别求出相应的概率,由此能求出X的分布列和数学期望Ex.
解答 解:由题意知旧球个数X的所有可能取值为3,4,5,6.
P(X=3)=$\frac{{C}_{3}^{3}}{{C}_{12}^{3}}$=$\frac{1}{220}$,
P(X=4)=$\frac{{C}_{3}^{2}{C}_{9}^{1}}{{C}_{12}^{3}}$=$\frac{27}{220}$,
P(X=5)=$\frac{{C}_{9}^{2}{C}_{3}^{1}}{{C}_{12}^{3}}$=$\frac{108}{220}$=$\frac{27}{55}$,
P(X=6)=$\frac{{C}_{9}^{3}}{{C}_{12}^{3}}$=$\frac{84}{220}=\frac{21}{55}$,
故X的分布列为:
| X | 3 | 4 | 5 | 6 |
| p | $\frac{1}{220}$ | $\frac{27}{220}$ | $\frac{27}{55}$ | $\frac{21}{55}$ |
点评 本题离散型随机变量的分布列和数学期望的求法,考查学生分析解决问题的能力,考查数据处理能力、运算求解能力,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
7.下列函数中,既是偶函数又在(0,+∞)上单调递减的是( )
| A. | y=-x | B. | y=cosx | C. | y=${x^{\frac{2}{5}}}$ | D. | y=-x2 |
8.某几何体的三视图如图所示,则该几何体的体积为( )
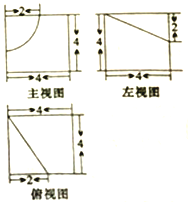

| A. | 64 | B. | 64-4π | C. | 64-8π | D. | 64-$\frac{4π}{3}$ |
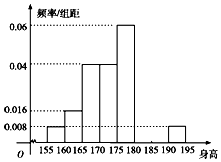 从某学校的1600名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,第六组的人数为4人.
从某学校的1600名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,第六组的人数为4人.