题目内容

已知矩形ABCD，AB=2AD=2，P为矩形ABCD内一点（包括矩形边界），
AP 
=x
AB
+y
AD
，则（x+1）2+（y+1）2的最大值为
 
．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：由矩形ABCD，AB=2AD=2，P为矩形ABCD内一点（包括矩形边界），
AP 
=x
AB
+y
AD
，求出变量x，y满足的约束条件，进而可得答案．
解答： 解：∵矩形ABCD，AB=2AD=2，P为矩形ABCD内一点（包括矩形边界），
AP 
=x
AB
+y
AD
，
则
0≤x≤1
0≤y≤1
，
故当x=y=1时，（x+1）2+（y+1）2取最大值为8，
故答案为：8
点评：本题主要考查了向量在几何中的应用，基本不等式的运用，属于中档题．
练习册系列答案
相关题目
将一根长为4米的木棍锯成两段，则锯成的两段都大于1米的概率是
 
．
已知
3
sin（x+40°）=cos（x+20°）+cos（x-20°），则tanx=
 
．
已知f（x）=
1-x
1+x
．若α∈（
π
2
，π），则f（-cosα）=
 
．
有4个不同的球，四个不同的盒子，把球全部放入盒内．恰有两个盒不放球，有多少种放法？答案
 
（结果用数字表示）
若sin（x+
π
6
）=
4
5
，则cos（x-
π
3
）=
 
．
（x-
1
x
）6展开式的常数项为
 
．
若复数
2+ai
1-i
（a∈R）是纯虚数（i是虚数单位），则a的值为
 
．
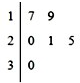车间共有6名工人，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数，日加工零件个数大于样本均值的工人为优秀工人．从该车间6名工人中，任取2人，则恰有1名优秀工人的概率为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网