题目内容
2．已知2a=3b=6c，k∈Z，不等式$\frac{a+b}{c}$＞k恒成立，则整数k的最大值为（ ）| A． | 6 | B． | 5 | C． | 3 | D． | 4 |
分析 根据指数幂和对数的运算性质，结合基本不等式即可得到结论．
解答 解：设2a=3b=6c=m，则a=log2m，b=log3m，c=log6m，
所以$\frac{a+b}{c}$=$\frac{lo{g}_{2}m+lo{g}_{3}m}{lo{g}_{6}m}$=$\frac{lg6}{lg2}$+$\frac{lg6}{lg3}$=$\frac{lg2+lg3}{lg2}$+$\frac{lg2+lg3}{lg3}$=2+$\frac{lg3}{lg2}$+$\frac{lg2}{lg3}$，
∵$\frac{lg3}{lg2}$+$\frac{lg2}{lg3}$＞2$\sqrt{\frac{lg3}{lg2}×\frac{lg2}{lg3}}$=2，$\frac{lg3}{lg2}$+$\frac{lg2}{lg3}$=log23+log32＜3，
∴4＜$\frac{a+b}{c}$＜5，
则整数k的最大值为4．
故选：D．
点评 本题主要考查与对数有关的恒成立问题，利用对数的运算法则结合基本不等式的性质是解决本题的关键．
练习册系列答案
相关题目
12．
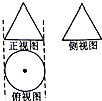一个几何体的三视图如图所示，其中正视图和侧视图都是边长为2的正三角形，那么这个几何体的体积为（ ）
一个几何体的三视图如图所示，其中正视图和侧视图都是边长为2的正三角形，那么这个几何体的体积为（ ）| A． | $\frac{\sqrt{3}}{3}π$ | B． | $\frac{\sqrt{2}}{2}π$ | C． | $\frac{\sqrt{2}}{4}π$ | D． | $\frac{π}{4}$ |
11．已知log3（x+y+4）＞log3（3x+y-2），若x-y＜λ恒成立，则λ的取值范围是（ ）
| A． | （-∞，10] | B． | （-∞，10） | C． | （10，+∞） | D． | [10，+∞） |
如图，抛物线的方程为y2=2px（p＞0），F为该抛物线的焦点，A是该抛物线的准线与x轴的交点，M是抛物线上一点，且满足MA⊥MF．