题目内容
12. 如图,抛物线的方程为y2=2px(p>0),F为该抛物线的焦点,A是该抛物线的准线与x轴的交点,M是抛物线上一点,且满足MA⊥MF.
如图,抛物线的方程为y2=2px(p>0),F为该抛物线的焦点,A是该抛物线的准线与x轴的交点,M是抛物线上一点,且满足MA⊥MF.(1)若p=2,求该抛物线的焦点坐标及准线方程;
(2)当p值变化时,△MAF的面积是否存在最小值?若存在,求出最小值,若不存在,说明理由.
分析 (1)由抛物线的焦点坐标公式和准线方程,即可得到;
(2)设出M的坐标和A,F的坐标,由两直线垂直的条件:斜率之积为-1和两点的斜率公式,解方程求得m,再由三角形的面积公式计算即可判断是否存在最小值.
解答 解:(1)当p=2时,抛物线y2=4x的焦点为F(1,0),准线方程为x=-1;
(2)设M(m,n),由题意可得A(-$\frac{p}{2}$,0),F($\frac{p}{2}$,0),
由MA⊥MF,可得kMF•kMA=-1,
即$\frac{n}{m-\frac{p}{2}}$•$\frac{n}{m+\frac{p}{2}}$=-1,即有n2=$\frac{{p}^{2}}{4}$-m2,
又n2=2pm,即有2pm=$\frac{{p}^{2}}{4}$-m2,
解得m=($\frac{\sqrt{5}}{2}$-1)p(负的舍去),
S△MAF=$\frac{1}{2}$|AF|•|n|=$\frac{1}{2}$p$\sqrt{2pm}$=$\frac{1}{2}$$\sqrt{\sqrt{5}-2}$p2.
该函数在(0,+∞)上为增函数,则△MAF的面积不存在最小值.
点评 本题考查抛物线的方程和性质,考查两直线垂直的条件:斜率之积为-1,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
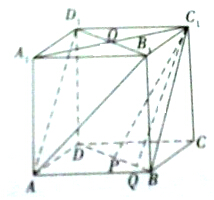 已知正方体ABCD-A1B1C1D1.
已知正方体ABCD-A1B1C1D1.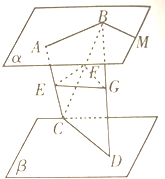 如图所示,已知平面α∥平面β,AB与CD是两条异面直线且AB?α,CD?β,如果E、F、G分别是AC、CB、BD的中点.求证:平面EFG∥α∥β.
如图所示,已知平面α∥平面β,AB与CD是两条异面直线且AB?α,CD?β,如果E、F、G分别是AC、CB、BD的中点.求证:平面EFG∥α∥β.