题目内容
11.已知log3(x+y+4)>log3(3x+y-2),若x-y<λ恒成立,则λ的取值范围是( )| A. | (-∞,10] | B. | (-∞,10) | C. | (10,+∞) | D. | [10,+∞) |
分析 要使不等式成立,则有$\left\{\begin{array}{l}x+y+4>0\\ 3x+y-2>0\\ x+y+4>3x+y-2\end{array}\right.$,即$\left\{\begin{array}{l}x+y+4>0\\ 3x+y-2>0\\ x<3\end{array}\right.$,设z=x-y,则y=x-z.作出不等式组对应的可行域如图所示的阴影部分(不包括左右边界),通过平移直线(目标函数)利用线性规划的有关知识即可得出.
解答 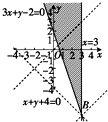 解:要使不等式成立,则有$\left\{\begin{array}{l}x+y+4>0\\ 3x+y-2>0\\ x+y+4>3x+y-2\end{array}\right.$,即$\left\{\begin{array}{l}x+y+4>0\\ 3x+y-2>0\\ x<3\end{array}\right.$,
解:要使不等式成立,则有$\left\{\begin{array}{l}x+y+4>0\\ 3x+y-2>0\\ x+y+4>3x+y-2\end{array}\right.$,即$\left\{\begin{array}{l}x+y+4>0\\ 3x+y-2>0\\ x<3\end{array}\right.$,
设z=x-y,则y=x-z.作出不等式组对应的可行域如图所示的阴影部分(不包括左右边界):
平移直线y=x-z,由图象可知当直线y=x-z经过点B时,直线在y轴上的截距最小,此时z最大,
由$\left\{\begin{array}{l}x+y+4=0\\ x=3\end{array}\right.$,解得$\left\{\begin{array}{l}y=-7\\ x=3\end{array}\right.$,代入z=x-y得z=x-y=3+7=10,
又因为可行域不包括点B,∴z<10,
∴要使x-y<λ恒成立,则λ的取值范围是λ≥10,即[10,+∞).
故选:D.
点评 本题考查了对数函数的单调性、线性规划的有关知识、不等式的性质,考查了数形结合思想方法、计算能力,属于中档题.

练习册系列答案
相关题目
6.已知在等比数列{an}中,a3+a6=6,a6+a9=$\frac{3}{4}$,则a8+a11等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{16}$ | D. | $\frac{3}{32}$ |
16.半径为1的球内最大圆柱的体积为( )
| A. | $\frac{2\sqrt{6}}{9}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{2\sqrt{3}}{3}$π | D. | $\frac{4\sqrt{3}}{9}$π |
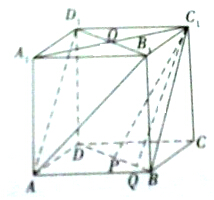 已知正方体ABCD-A1B1C1D1.
已知正方体ABCD-A1B1C1D1.