题目内容
17.已知△ABC的三边a,b,c和其面积S满足S=c2-(a-b)2,则tanC=$\frac{8}{15}$.分析 由已知等式及余弦定理可解得:$\frac{1-cosC}{sinC}$=$\frac{1}{4}$,利用倍角公式及同角三角函数关系式可求tan$\frac{C}{2}$=$\frac{1}{4}$,利用倍角公式即可求得tanC的值.
解答 解:∵由题意可得:S=c2-(a2+b2)+2ab=-2abcosC+2ab=2ab(1-cos C)=$\frac{1}{2}$absinC,
∴解得:$\frac{1-cosC}{sinC}$=$\frac{1}{4}$,
∴$\frac{2si{n}^{2}\frac{C}{2}}{2sin\frac{C}{2}cos\frac{C}{2}}$=$\frac{1}{4}$,
∴tan$\frac{C}{2}$=$\frac{1}{4}$,tanC=$\frac{2tan\frac{C}{2}}{1-ta{n}^{2}\frac{C}{2}}$=$\frac{2×\frac{1}{4}}{1-(\frac{1}{4})^{2}}$=$\frac{8}{15}$.
故答案为:$\frac{8}{15}$.
点评 本题主要考查了余弦定理,倍角公式及同角三角函数关系式的应用,属于基本知识的考查.

练习册系列答案
相关题目
7.定积分${∫}_{1}^{e}$($\frac{1}{x}$+2)dx的值为( )
| A. | 2e+1 | B. | 2e-1 | C. | e-2 | D. | 2e-2 |
6.已知在等比数列{an}中,a3+a6=6,a6+a9=$\frac{3}{4}$,则a8+a11等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{16}$ | D. | $\frac{3}{32}$ |
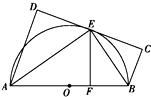 如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.
如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.